题目内容
5.解方程:(1)(x+1)(x-2)=x+1
(2)$\sqrt{2}$x2-4x=4$\sqrt{2}$.
分析 (1)方程整理后,利用因式分解法求出解即可;
(2)方程整理后,利用公式法求出解即可.
解答 解:(1)方程整理得:(x+1)(x-2)-(x+1)=0,
分解因式得:(x+1)(x-2-1)=0,
解得:x1=-1,x2=3;
(2)方程整理得:$\sqrt{2}$x2-4x-4$\sqrt{2}$=0,
这里a=$\sqrt{2}$,b=-4,c=-4$\sqrt{2}$,
∵△=16+16=32,
∴x=$\frac{4±4\sqrt{2}}{2\sqrt{2}}$=$\sqrt{2}$±2,
解得:x1=$\sqrt{2}$+2,x2=$\sqrt{2}$-2.
点评 此题考查了解一元二次方程-因式分解法,以及公式法,熟练掌握各种解法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.16的平方根是( )
| A. | 4 | B. | 8 | C. | ±2 | D. | ±4 |
13.在-1,π,$\sqrt{2}$,-$\sqrt{81}$中,无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,a∥b,若∠2=130°,则∠1=50°.
如图,a∥b,若∠2=130°,则∠1=50°.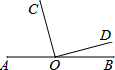 如图,点O是直线AB上一点,OC⊥OD,∠AOC:∠BOD=5:1,那么∠AOC的度数是75°.
如图,点O是直线AB上一点,OC⊥OD,∠AOC:∠BOD=5:1,那么∠AOC的度数是75°. 实数a,b在数轴上所对应的点的位置如图所示,用“<、>、=”等符号连接以下数字:2a<0,a+b>0,-|b-a|<0.
实数a,b在数轴上所对应的点的位置如图所示,用“<、>、=”等符号连接以下数字:2a<0,a+b>0,-|b-a|<0.