题目内容
12.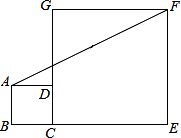 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是( )| A. | $\frac{3}{2}$$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\frac{3}{5}$$\sqrt{5}$ | D. | 2 |
分析 作CH⊥AF,垂足为H.根据△ADK∽△FGK,求出KF的长,再根据△CHK∽△FGK,求出CH的长.
解答 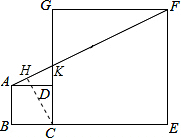 解:作CH⊥AF,垂足为H.
解:作CH⊥AF,垂足为H.
∵CD=BC=1,
∴GD=3-1=2,
∵△ADK∽△FGK,
∴$\frac{DK}{GK}$=$\frac{AD}{GF}$,
即$\frac{DK}{GK}$=$\frac{1}{3}$,
∴DK=2×$\frac{1}{4}$=$\frac{1}{2}$,GK=2×$\frac{3}{4}$=$\frac{3}{2}$,
∴KF=$\sqrt{(\frac{3}{2})^{2}+{3}^{2}}$=$\frac{3\sqrt{5}}{2}$,
∵△CHK∽△FGK,
∴$\frac{CH}{GF}$=$\frac{CK}{FK}$,
∴$\frac{CH}{3}$=$\frac{1+\frac{1}{2}}{\frac{3\sqrt{5}}{2}}$,
∴CH=$\frac{3\sqrt{5}}{5}$.
故选C.
点评 本题考查了勾股定理,利用勾股定理求出三角形的边长,再构造相似三角形是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
20.某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如下表所示:
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可毛获利润共2.7万元.[毛利润=(售价-进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
| 国外品牌 | 国内品牌 | |
| 进价(元/部) | 4400 | 2000 |
| 售价(元/部) | 5000 | 2500 |
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
17.若关于x的不等式ax+3>0的解集为x<3,则关于m的不等式m+2a<1的解为( )
| A. | m<3 | B. | m<-3 | C. | m>-3 | D. | m>-2 |
1.如图,是测量一物体体积的过程:(1mL=1cm3)
步骤一:将300ml的水装进一个容量为500mL的杯子中;
步骤二:将四颗相同的玻璃球放入水中,结果水没有满;
步骤三:再加一颗同样的玻璃球放入水中,结果水满溢出.
根据以上过程,推测这样一颗玻璃球的体积为下列范围内的( )

步骤一:将300ml的水装进一个容量为500mL的杯子中;
步骤二:将四颗相同的玻璃球放入水中,结果水没有满;
步骤三:再加一颗同样的玻璃球放入水中,结果水满溢出.
根据以上过程,推测这样一颗玻璃球的体积为下列范围内的( )

| A. | 10cm3以上,20cm3以下 | B. | 20cm3以上,30cm3以下 | ||
| C. | 30cm3以上,40cm3以下 | D. | 40cm3以上,50cm3以下 |
 如图,已知四边形ABCD是正方形,点E在DC边上,点F在CB边的延长线上,且DE=BF,连接AE,AF,EF.
如图,已知四边形ABCD是正方形,点E在DC边上,点F在CB边的延长线上,且DE=BF,连接AE,AF,EF. 如图所示,直线AB、CD相交于点O,∠DOE:∠BOD=3:2,OF平分∠AOE,若∠AOC=24°,则∠EOF的度数.
如图所示,直线AB、CD相交于点O,∠DOE:∠BOD=3:2,OF平分∠AOE,若∠AOC=24°,则∠EOF的度数.