题目内容
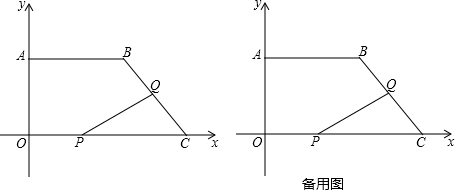
2. 如图所示,直线AB、CD相交于点O,∠DOE:∠BOD=3:2,OF平分∠AOE,若∠AOC=24°,则∠EOF的度数.
如图所示,直线AB、CD相交于点O,∠DOE:∠BOD=3:2,OF平分∠AOE,若∠AOC=24°,则∠EOF的度数.
分析 根据对顶角相等,得到∠BOD=24°,因为∠DOE:∠BOD=3:2,所以∠BOE=60°,根据平角∠AOE=180°-∠BOE=120°,因为OF平分∠AOE,所以∠EOF=$\frac{1}{2}∠AOE=6{0}^{°}$.
解答 解:∵∠BOD=∠AOC,∠AOC=24°,
∴∠BOD=24°,
∵∠DOE:∠BOD=3:2,
∴∠BOE=60°,
∴∠AOE=180°-∠BOE=120°,
∵OF平分∠AOE,
∴∠EOF=$\frac{1}{2}∠AOE=6{0}^{°}$.
点评 本题考查了对顶角、邻补角,解决本题的关键是明确对顶角相等,角平分线的性质.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
12.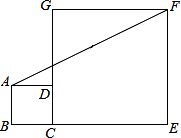 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是( )
 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是( )| A. | $\frac{3}{2}$$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\frac{3}{5}$$\sqrt{5}$ | D. | 2 |
17.如果(x+m)与(x+5)的乘积中不含x的一次项,则m的值为( )
| A. | -5 | B. | 5 | C. | 0 | D. | 3 |
7.将点A(2,1)沿x轴向左平移4个单位长度得到点A′,则点A′的坐标是( )
| A. | (-2,1) | B. | (2,-3) | C. | (2,5) | D. | (6,1) |