题目内容
20.某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如下表所示:| 国外品牌 | 国内品牌 | |
| 进价(元/部) | 4400 | 2000 |
| 售价(元/部) | 5000 | 2500 |
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
分析 (1)设商场计划购进甲种手机x部,乙种手机y部,根据两种手机的购买金额为14.8万元和两种手机的销售利润为2.7万元建立方程组求出其解即可;
(2)设甲种手机减少a部,则乙种手机增加3a部,表示出购买的总资金,由总资金部超过15.6万元建立不等式就可以求出a的取值范围,再设销售后的总利润为W元,表示出总利润与a的关系式,由一次函数的性质就可以求出最大利润.
解答 解:(1)设商场计划购进国外品牌手机x部,国内品牌手机y部,由题意,得:
$\left\{\begin{array}{l}{0.44x+0.2y=14.8}\\{0.06x+0.05y=2.7}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=20}\\{y=30}\end{array}\right.$,
答:商场计划购进国外品牌手机20部,国内品牌手机30部;
(2)设国外品牌手机减少a部,则国内手机品牌增加3a部,由题意,得:
0.44(20-a)+0.2(30+3a)≤15.6,
解得:a≤5,
设全部销售后获得的毛利润为w万元,由题意,得:
w=0.06(20-a)+0.05(30+3a)=0.09a+2.7,
∵k=0.09>0,
∴w随a的增大而增大,
∴当a=5时,w最大=3.15,
答:当该商场购进国外品牌手机15部,国内品牌手机45部时,全部销售后获利最大,最大毛利润为3.15万元.
点评 本题考查了列二元一次方程组解实际问题的运用,列一元一次不等式解实际问题的运用及一次函数的性质的运用,解答本题时灵活运用一次函数的性质求解是关键.

练习册系列答案
相关题目
11. 如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )
如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )
 如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )
如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{2}{3}$ |
8.在-$\frac{1}{2}$,0,$\frac{1}{3}$,-1这四个数中,最小的数是( )
| A. | -$\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{3}$ | D. | -1 |
5.抛物线y=ax2+bx+c上部分点的横坐标x、纵坐标y的对应值如下表:
从上表可知,下列说法中正确的有(填写序号)( )
①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最值为6;③抛物线的对称轴是x=$\frac{1}{2}$;④在对称轴左侧,y随x的增大而增大.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最值为6;③抛物线的对称轴是x=$\frac{1}{2}$;④在对称轴左侧,y随x的增大而增大.
| A. | ①④ | B. | ②③ | C. | ①③④ | D. | ③④ |
12.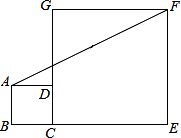 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是( )
 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是( )| A. | $\frac{3}{2}$$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\frac{3}{5}$$\sqrt{5}$ | D. | 2 |
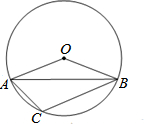 如图,在⊙O中,已知∠OAB=21.5°,则∠C的度数为111.5°.
如图,在⊙O中,已知∠OAB=21.5°,则∠C的度数为111.5°.