题目内容
已知二次函数y=ax2+bx+c图象经过直线y=-3x+3与x轴,y轴的交点,对称轴为直线x=-1,设函数图象与x轴交点为A,B,与y轴交点为C,顶点为D,求四边形ABCD的面积.
考点:抛物线与x轴的交点
专题:
分析:先求出A、C的坐标,再求出二次函数y=ax2+bx+c的解析式,连接CE,根据三角形的面积公式即可得出结论.
解答: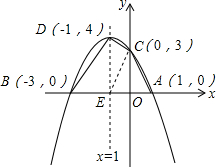 解:∵A、C为直线y=-3x+3与x轴,y轴的交点,
解:∵A、C为直线y=-3x+3与x轴,y轴的交点,
∴A(1,0),C(0,3),
∵二次函数的对称轴为直线x=-1,
∴B(-3,0).
∵二次函数y=ax2+bx+c图象经过A、B、C,且对称轴为x=-1,
∴
,
解得
,
∴二次函数的解析式为y=-x2-2x+3,
∴顶点D(-1,4).
连接CE,
∴S四边形ABCD=S△BDE+S△CDE+S△ACE=
×4×2+
×4×1+
×2×3=9.
 解:∵A、C为直线y=-3x+3与x轴,y轴的交点,
解:∵A、C为直线y=-3x+3与x轴,y轴的交点,∴A(1,0),C(0,3),
∵二次函数的对称轴为直线x=-1,
∴B(-3,0).
∵二次函数y=ax2+bx+c图象经过A、B、C,且对称轴为x=-1,
∴
|
解得
|
∴二次函数的解析式为y=-x2-2x+3,
∴顶点D(-1,4).
连接CE,
∴S四边形ABCD=S△BDE+S△CDE+S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是抛物线与x轴的交点,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
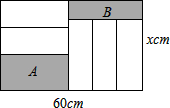 如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为y(cm).
如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为y(cm). 已知二次函数y=ax2+bx+c的图象如图,则点A(ac,bc)在第
已知二次函数y=ax2+bx+c的图象如图,则点A(ac,bc)在第 一辆卡车装满货物后,它的高比宽多两米,且恰好通过如图所示的隧道,(上部为半圆形).卡车有多高?(结果精确到0.1m).
一辆卡车装满货物后,它的高比宽多两米,且恰好通过如图所示的隧道,(上部为半圆形).卡车有多高?(结果精确到0.1m). 从正方形ABCD的顶点A作∠EAF=45°,交DC于点F,BC于点E.
从正方形ABCD的顶点A作∠EAF=45°,交DC于点F,BC于点E.