题目内容
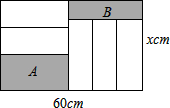 如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为y(cm).
如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为y(cm).(1)从图可知,每个小长方形较长的一边长
(2)分别用含x,y的代数式表示阴影A,B的面积,并计算阴影A,B的面积差.
考点:整式的混合运算,列代数式
专题:
分析:(1)根据大长方形的长是60cm和小长方形的宽是ycm得出即可;
(2)先分别求出A、B的长和宽,即可求出面积.
(2)先分别求出A、B的长和宽,即可求出面积.
解答:解:(1)从图可知,每个小长方形较长的一边长是(60-3y)cm,
故答案为:(60-3y);
(2)阴影部分A的面积是(60-3y)(x-2y)cm2,阴影部分B的面积是3y[x-(60-3y)]cm2,
所以阴影A,B的面积差是:
(60-3y)(x-2y)-3y[x-(60-3y)]
=60x-120y-3xy+6y2-3xy+180y-9y2
=-3y2-6xy+120y,
即阴影A,B的面积差是(-3y2-6xy+120y)cm2.
故答案为:(60-3y);
(2)阴影部分A的面积是(60-3y)(x-2y)cm2,阴影部分B的面积是3y[x-(60-3y)]cm2,
所以阴影A,B的面积差是:
(60-3y)(x-2y)-3y[x-(60-3y)]
=60x-120y-3xy+6y2-3xy+180y-9y2
=-3y2-6xy+120y,
即阴影A,B的面积差是(-3y2-6xy+120y)cm2.
点评:本题考查了整式的混合运算的应用,解此题的关键是能根据题意列出算式.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目