题目内容
 从正方形ABCD的顶点A作∠EAF=45°,交DC于点F,BC于点E.
从正方形ABCD的顶点A作∠EAF=45°,交DC于点F,BC于点E.(1)问DF+BE=EF吗?
(2)过点A作AP⊥EF于P,求证:AP=AB.
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)将△ABE绕点A逆时针旋转90°得到△ADH,根据旋转的性质可得BE=DH,AE=AH,∠BAE=∠DAH,然后求出∠EAF=∠HAF=45°,再利用“边角边”证明△AEF和△AHF全等,根据全等三角形对应边相等可得EF=HF,再根据DF+DH=FH等量代换即可得证;
(2)根据全等三角形对应边上的高相等可得AP=AD,再根据AB=AD等量代换即可得证.
(2)根据全等三角形对应边上的高相等可得AP=AD,再根据AB=AD等量代换即可得证.
解答: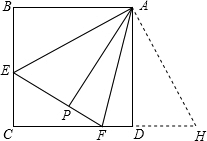 (1)解:如图,将△ABE绕点A逆时针旋转90°得到△ADH,
(1)解:如图,将△ABE绕点A逆时针旋转90°得到△ADH,
由旋转的性质得,BE=DH,AE=AH,∠BAE=∠DAH,
∵∠EAF=45°,
∴∠EAF=∠HAF=45°,
在△AEF和△AHF中,
,
∴△AEF≌△AHF(SAS),
∴EF=HF,
∵DF+DH=FH,
∴DF+BE=EF;
(2)∵△AEF≌△AHF,AP、AD分别是△AEF和△AHF对应边上的高,
∴AP=AD,
∵AB=AD,
∴AP=AB.
 (1)解:如图,将△ABE绕点A逆时针旋转90°得到△ADH,
(1)解:如图,将△ABE绕点A逆时针旋转90°得到△ADH,由旋转的性质得,BE=DH,AE=AH,∠BAE=∠DAH,
∵∠EAF=45°,
∴∠EAF=∠HAF=45°,
在△AEF和△AHF中,
|
∴△AEF≌△AHF(SAS),
∴EF=HF,
∵DF+DH=FH,
∴DF+BE=EF;
(2)∵△AEF≌△AHF,AP、AD分别是△AEF和△AHF对应边上的高,
∴AP=AD,
∵AB=AD,
∴AP=AB.
点评:本题考查了正方形的性质,全等三角形的判定与性质,利用旋转作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目
下表是某报纸公布的世界人口数据情况:表中的变量( )
| 年份 | 1957 | 1974 | 1987 | 1999 | 2010 |
| 人口数 | 30亿 | 40亿 | 50亿 | 60亿 | 70亿 |
| A、仅有一个,是时间(年份) |
| B、仅有一个,是人口数 |
| C、有两个,一个是人口数,另一个是时间(年份) |
| D、一个也没有 |
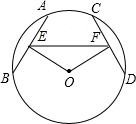 如图所示,⊙O中,AB、CD是弦,点E、F是AB、CD的中点,并且AB=CD.
如图所示,⊙O中,AB、CD是弦,点E、F是AB、CD的中点,并且AB=CD. 如图,在△ABC中(AB>BC),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,求AC和AB的长.
如图,在△ABC中(AB>BC),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,求AC和AB的长. 如图,AB、CD相交于点O,△AOB≌△DOC,且∠A=80°,∠DOC=30°,BO=23,AO=18,求∠DC0的度数和BD的长度.
如图,AB、CD相交于点O,△AOB≌△DOC,且∠A=80°,∠DOC=30°,BO=23,AO=18,求∠DC0的度数和BD的长度.