题目内容
13.(1)计算 $|{-\sqrt{3}}|-{({π-3.14})^0}-\sqrt{12}+{({\frac{1}{2}})^{-1}}$(2)化简 $(\frac{a}{{{a^2}-{b^2}}}-\frac{1}{a+b})÷\frac{b}{b-a}$.
分析 (1)先化简绝对值,二次根式,计算0指数幂,负指数幂,再算加减;
(2)先通分算减法,再算除法.
解答 解:(1)原式=$\sqrt{3}$-1-2$\sqrt{3}$+2
=1-$\sqrt{3}$;
(2)原式=$\frac{b}{(a+b)(a-b)}$•$\frac{b-a}{b}$
=-$\frac{1}{a+b}$.
点评 此题考查分式的混合运算,实数的混合运算,掌握运算顺序于计算方法是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.若-x3ym与xny是同类项,则m+n的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.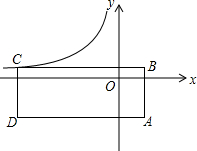 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{{{k^2}+3k-3}}{x}$的图象上若点A的坐标为($\sqrt{5}$,$-\sqrt{5}$),则k的值为( )
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{{{k^2}+3k-3}}{x}$的图象上若点A的坐标为($\sqrt{5}$,$-\sqrt{5}$),则k的值为( )
 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{{{k^2}+3k-3}}{x}$的图象上若点A的坐标为($\sqrt{5}$,$-\sqrt{5}$),则k的值为( )
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{{{k^2}+3k-3}}{x}$的图象上若点A的坐标为($\sqrt{5}$,$-\sqrt{5}$),则k的值为( )| A. | -2或-1 | B. | -2或1 | C. | -5或1 | D. | 5或1 |
3.在有理数:-2,-(-2),|-2|,-|-2|中,负数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
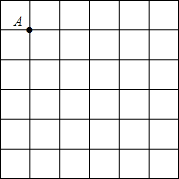 作图题:如图,在6×6的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形.
作图题:如图,在6×6的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形.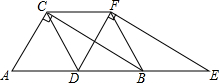 两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC不动,将△DEF沿射线AB方向平移,当D点移动到AB的中点时,
两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC不动,将△DEF沿射线AB方向平移,当D点移动到AB的中点时,