题目内容
2.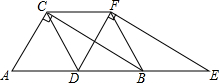 两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC不动,将△DEF沿射线AB方向平移,当D点移动到AB的中点时,
两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC不动,将△DEF沿射线AB方向平移,当D点移动到AB的中点时,(1)请你猜想四边形CDBF的形状,并说明理由.
(2)求四边形CDBF的面积.
分析 (1)先根据图形平移的性质得出AC∥DF,FC∥ED,故四边形CDBF是平行四边形.再根据DF∥AC,∠ACB=90°可得出CB⊥DF,由此可得出结论;
(2)先根据勾股定理求出BC的长,再由平移的性质得出DF的长,由菱形的面积公式即可得出结论.
解答 解:(1)猜想:四边形CDBF是菱形.
∵将△DEF沿射线AB方向移动,
∴AC∥DF,FC∥ED.
∴四边形CDBF是平行四边形.
∵DF∥AC,∠ACB=90°,
∴CB⊥DF,
∴四边形CDBF是菱形;
(2)∵∠A=60°,∠ACB=90°,AC=1,
∴∠ABC=30°,
∴BC=$\sqrt{{AB}^{2}-{AC}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$.
∵△DFE由△ACB平移而成,
∴DF=AC=1.
∵由(1)知,四边形CDBF是菱形,
∴S四边形CDBF=$\frac{1}{2}$DF•BC=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查的是菱形的判定与性质,涉及到图形平移的性质及菱形的判定定理,难度适中.

练习册系列答案
相关题目
12.下列函数中,自变量x的取值范围是x>-2的是( )
| A. | y=x+2 | B. | y=$\frac{1}{x+2}$ | C. | y=$\sqrt{x+2}$ | D. | y=$\frac{x-2}{\sqrt{x+2}}$ |
 如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,则∠DAE=15度.
如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,则∠DAE=15度.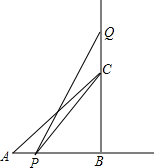 如图,在△ABC中,∠B=90°,AB=BC=10cm,点P从点A出发沿射线AB以1cm/s的速度作直线运动,点Q从点C出发沿射线BC以2cm/s的速度作直线运动.如果P,Q分别从A,B同时出发,经过几秒,S△PCQ=$\frac{12}{25}$S△ABC?
如图,在△ABC中,∠B=90°,AB=BC=10cm,点P从点A出发沿射线AB以1cm/s的速度作直线运动,点Q从点C出发沿射线BC以2cm/s的速度作直线运动.如果P,Q分别从A,B同时出发,经过几秒,S△PCQ=$\frac{12}{25}$S△ABC?