题目内容
1.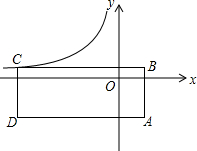 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{{{k^2}+3k-3}}{x}$的图象上若点A的坐标为($\sqrt{5}$,$-\sqrt{5}$),则k的值为( )
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{{{k^2}+3k-3}}{x}$的图象上若点A的坐标为($\sqrt{5}$,$-\sqrt{5}$),则k的值为( )| A. | -2或-1 | B. | -2或1 | C. | -5或1 | D. | 5或1 |
分析 设C(x,y).根据矩形的性质、点A的坐标分别求出B($\sqrt{5}$,y)、D(x,-$\sqrt{5}$);根据“矩形ABCD的对角线BD经过坐标原点”及直线AB的几何意义求得xy=-5①,又点C在反比例函数y=$\frac{{{k^2}+3k-3}}{x}$的图象上,所以将点C的坐标代入其中求得xy=k2+3k-3②;联立①②解关于k的一元二次方程即可.
解答 解:设C(x,y).
∵四边形ABCD是矩形,点A的坐标为($\sqrt{5}$,-$\sqrt{5}$),
∴B($\sqrt{5}$,y)、D(x,-$\sqrt{5}$);
∵矩形ABCD的对角线BD经过坐标原点,
∴设直线BD的函数关系式为:y=mx,
∵B($\sqrt{5}$,y)、D(x,-$\sqrt{5}$),
∴k=$\frac{y}{\sqrt{5}}$,k=$\frac{-\sqrt{5}}{x}$,
∴$\frac{y}{\sqrt{5}}$=$\frac{-\sqrt{5}}{x}$,即xy=-5;①
又∵点C在反比例函数y=$\frac{{{k^2}+3k-3}}{x}$的图象上,
∴xy=k2+3k-3,②
由①②,得
k2+3k+2=0,即(k+1)(k+2)=0,
∴k=-1或k=-2,
故选A.
点评 本题主要考查了待定系数法求反比例函数解析式、矩形的性质.解答此题的难点是根据C(x,y)求得B、D两点的坐标,求得xy的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列函数中,自变量x的取值范围是x>-2的是( )
| A. | y=x+2 | B. | y=$\frac{1}{x+2}$ | C. | y=$\sqrt{x+2}$ | D. | y=$\frac{x-2}{\sqrt{x+2}}$ |
9.计算$\root{3}{27}$的结果是( )
| A. | ±3 | B. | 3 | C. | 3$\sqrt{3}$ | D. | $\sqrt{3}$ |
16.已知反比例函数y=$\frac{10}{x}$,当1<x<2时,y的取值范围是( )
| A. | 0<x<5 | B. | 1<y<2 | C. | 5<y<10 | D. | y>10 |
 如图,已知点O在直线AB上,OD平分∠AOC,OE平分∠BOC,求∠DOE的度数.
如图,已知点O在直线AB上,OD平分∠AOC,OE平分∠BOC,求∠DOE的度数. 二次函数y=x2+4x+3的图象与x轴交于A、B两点,与y轴交于D点,顶点为C,求:四边形ACBD的面积.
二次函数y=x2+4x+3的图象与x轴交于A、B两点,与y轴交于D点,顶点为C,求:四边形ACBD的面积.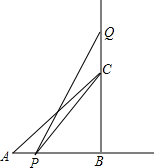 如图,在△ABC中,∠B=90°,AB=BC=10cm,点P从点A出发沿射线AB以1cm/s的速度作直线运动,点Q从点C出发沿射线BC以2cm/s的速度作直线运动.如果P,Q分别从A,B同时出发,经过几秒,S△PCQ=$\frac{12}{25}$S△ABC?
如图,在△ABC中,∠B=90°,AB=BC=10cm,点P从点A出发沿射线AB以1cm/s的速度作直线运动,点Q从点C出发沿射线BC以2cm/s的速度作直线运动.如果P,Q分别从A,B同时出发,经过几秒,S△PCQ=$\frac{12}{25}$S△ABC?