题目内容
9. 已知,如图中,AB为⊙O的切线,B为切点,BC为弦,∠CBA=40°,D为⊙O上一动点,且不与B、C重合,则∠CDB=40°或140°.
已知,如图中,AB为⊙O的切线,B为切点,BC为弦,∠CBA=40°,D为⊙O上一动点,且不与B、C重合,则∠CDB=40°或140°.
分析 画出图形,连接OB、OC,则OB⊥AB,求出∠OBC,∠BOC,继而分类讨论,可得出∠CDB及∠CD′B的度数.
解答  解:如图,连接OB、OC,
解:如图,连接OB、OC,
∵AB为⊙O的切线,B为切点,
∴OB⊥AB,
∵∠CBA=40°,
∴∠OBC=50°,
∵OB=OC,
∴∠OCB=∠OBC=50°,
∴∠BOC=180°-∠OCB-∠OBC=80°.
①当点D在优弧BC上时,
∠CDB=$\frac{1}{2}$∠BOC=40°;
②当点D′在劣弧BC上时,
∠CDB=180°-40°=140°.
综上可得:∠CDB=40°或140°.
故答案是:40°或140°.
点评 本题考查了切线的性质,需要用到的知识点为:①圆的切线垂直于经过切点的半径,②圆周角定理,③圆内接四边形的对角互补.

练习册系列答案
相关题目
4.2015年4月30日新的津蓟铁路市郊列车取代了传统的绿皮车,实现列车升级,并且升级后列车从天津到蓟县的行驶路程比原路程缩短25公里,实现升级后列车的行驶速度是原来速度的$\frac{10}{7}$倍,从天津到蓟县的行驶时间缩短了1小时.若列车升级前绿皮车从天津到蓟县的行驶路程为175公里,则列车升级后的速度为( )
| A. | 45公里/小时 | B. | 60公里/小时 | C. | 90公里/小时 | D. | 100公里/小时 |
19.某商店把一件商品按进价增加20%作为标价,可是总卖不出去,后来老板把标价降低20%,以96元的价格出售,很快就卖出了,则老板卖出这件商品的盈亏情况是( )
| A. | 赚2元 | B. | 不亏不赚 | C. | 亏2元 | D. | 亏4元 |
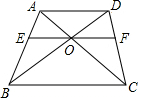 四边形ABCD中,AD∥BC,AC与BD相交于O点,过O点作EF∥BC分别交AB、CD于E,F两点,求证:
四边形ABCD中,AD∥BC,AC与BD相交于O点,过O点作EF∥BC分别交AB、CD于E,F两点,求证: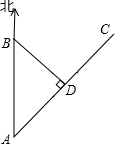 如图所示,沿海城市B的正南方向A处有一台风中心,沿AC的方向以30km/h的速度移动3小时后到达D处.已知A距台风中心最短的距离BD为120km,求AB间的距离.
如图所示,沿海城市B的正南方向A处有一台风中心,沿AC的方向以30km/h的速度移动3小时后到达D处.已知A距台风中心最短的距离BD为120km,求AB间的距离. 某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.
某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里. 如图,一个直立的油桶高0.8米,在顶部的一个开口中将一根长1米的木杆斜着插入桶内,上端正好与桶面相平,抽出后看到杆上油浸到部分长0.8m,则油桶内油面的高度是0.64m.
如图,一个直立的油桶高0.8米,在顶部的一个开口中将一根长1米的木杆斜着插入桶内,上端正好与桶面相平,抽出后看到杆上油浸到部分长0.8m,则油桶内油面的高度是0.64m.