题目内容
20. 设函数y=-x2+2(m-1)x+m+1的图象如图所示,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为2.
设函数y=-x2+2(m-1)x+m+1的图象如图所示,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为2.
分析 设点A的坐标为(-a,0),点B的坐标为(3a,0)然后利用根与系数的关系列出关于m的方程,从而可求得m的值.
解答 解:设点A的坐标为(-a,0),点B的坐标为(3a,0).
由根与系数的关系可知:-a+3a=2(m-1),-a•3a=-(m+1),
整理得:a=m-1,3a2=m+1
将a=m-1代入得:3(m-1)2=m+1.
解得:m=2或m=$\frac{1}{3}$(舍去).
故答案为:2.
点评 本题主要考查的是抛物线与x轴的交点,利用根与系数的关系得到关于m的方程是解题关键

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
13.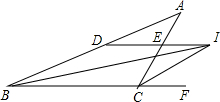 如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )
如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )
 如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )
如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )| A. | 2cm | B. | 5cm | C. | 4cm | D. | 5cm |
 如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,求∠A的度数.
如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,求∠A的度数. 若要使如图所示的平面展开图按虚线折叠成正方体后,相对的面上的两个数之和为6,则x=5,y=4.
若要使如图所示的平面展开图按虚线折叠成正方体后,相对的面上的两个数之和为6,则x=5,y=4. 如图所示,求阴影部分的面积.
如图所示,求阴影部分的面积.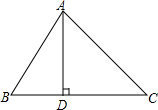 如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.