题目内容
16. 如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为18°,且OA=OB=3m.
如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为18°,且OA=OB=3m.(1)求此时另一端A离地面的距离(精确到0.1m);
(2)跷动AB,使端点A碰到地面,请画出点A运动的路线(写出画法,并保留画图痕迹),并求出点A运动路线的长.
(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
分析 (1)过点A作地面的垂线,垂足为C,在Rt△ABC中,根据正弦函数即可求得;
(2)以点O为圆心,OA长为半径画弧,交地面于点D,则$\widehat{AD}$就是端点A运动的路线;根据弧长公式即可求得.
解答 解:(1)过点A作地面的垂线,垂足为C,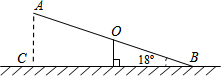
在Rt△ABC中,∠ABC=18°,
∴AC=AB•sin∠ABC
=6•sin18°
≈6×0.31≈1.9.
答:另一端A离地面的距离约为1.9 m.
(2)画法:以点O为圆心,OA长为半径画弧,交地面于点D,则$\widehat{AD}$就是端点A运动的路线.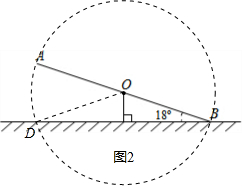
端点A运动路线的长为$\frac{2×18×π×3}{180}$=$\frac{3π}{5}$(m).
答:端点A运动路线的长为$\frac{3π}{5}$m.
点评 本题考查了学生利用三角函数解决实际问题的能力以及弧长的计算.这就要求学生把实际问题转化为直角三角形的问题,利用三角函数解决问题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
6.函数y=kx+b(k≠0)中,当x的值增加2时,y的值减小3,则k的值为( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | -2 | D. | -3 |
4. 如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于( )
如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于( )
 如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于( )
如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于( )| A. | 150° | B. | 80° | C. | 100° | D. | 115° |
1. 如图,在△ABC中,∠C=36°,将△ABC绕点A逆时针旋转60°得到△AED,AD与BC交于点F,则∠AFC的度数为( )
如图,在△ABC中,∠C=36°,将△ABC绕点A逆时针旋转60°得到△AED,AD与BC交于点F,则∠AFC的度数为( )
 如图,在△ABC中,∠C=36°,将△ABC绕点A逆时针旋转60°得到△AED,AD与BC交于点F,则∠AFC的度数为( )
如图,在△ABC中,∠C=36°,将△ABC绕点A逆时针旋转60°得到△AED,AD与BC交于点F,则∠AFC的度数为( )| A. | 84° | B. | 80° | C. | 60° | D. | 90° |
5.二元一次方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ |
6.如果3a7xby+7和-7a2-4yb2x是同类项,则x、y的值是( )
| A. | x=-3,y=2 | B. | x=-2,y=3 | C. | x=2,y=-3 | D. | x=3,y=-2 |