题目内容
4. 如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于( )
如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于( )| A. | 150° | B. | 80° | C. | 100° | D. | 115° |
分析 先利用折叠的性质得到∠BFE=∠2,再利用平角的定义计算出∠BFE=65°,然后根据两直线平行,同旁内角互补求解.
解答 解: ∵矩形ABCD沿EF对折,
∵矩形ABCD沿EF对折,
∴∠BFE=∠2,
∴∠BFE=$\frac{1}{2}$(180°-∠1)=$\frac{1}{2}$×(180°-50°)=65°,
∵AD∥BC,
∴∠AEF+∠BFE=180°,
∴∠AEF=180°-65°=115°.
故选D.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了折叠的性质.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
14. 如图,已知一次函数y=kx+b的图象,当x<0,y的取值范围是( )
如图,已知一次函数y=kx+b的图象,当x<0,y的取值范围是( )
 如图,已知一次函数y=kx+b的图象,当x<0,y的取值范围是( )
如图,已知一次函数y=kx+b的图象,当x<0,y的取值范围是( )| A. | y>0 | B. | y<0 | C. | y<-2 | D. | 2<y<0 |
12.下列各题中是无理数的是( )
| A. | $\sqrt{9}$ | B. | $\frac{π}{2}$ | C. | $\frac{24}{7}$ | D. | $\root{3}{8}$ |
13.从下列不等式中选择一个与x+1≥2组成不等式组,如果要使该不等式组的解集为x≥1,那么可以选择的不等式可以是( )
| A. | x>-1 | B. | x>2 | C. | x<-1 | D. | x<2 |
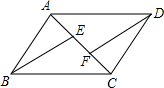 已知平行四边形ABCD中,BE∥DF,求证:AE=CF.
已知平行四边形ABCD中,BE∥DF,求证:AE=CF. 如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为18°,且OA=OB=3m.
如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为18°,且OA=OB=3m.