题目内容
8.如图,已知两条直线a∥b,直线a、b间的距离为h,点M、N在直线a上,MN=x;点P在直线b上,并且x+h=40.(1)记△PMN的面积为S,
①求S与x的函数关系,并求出MN的长为多少时△PMN的面积最大?最大面积是多少?
②当△PMN的面积最大时,能过出∠PMN的正切值吗?为什么?
(2)①请你用尺规作图的方法确定△PMN的周长最小时点P的位置(要求不写作法,但保留作图痕迹);并判断△PMN的形状;
②直接写出当△PMN的面积最大时这个最小周长的值;
(3)请你在(2)②中得到的△PMN内求一点P,使得AP+AM+AN的和最小,求出AP+AM+AN和的最小值.
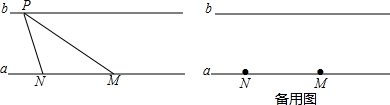
分析 (1)①根据x+h=40得出h=40-x,再由三角形的面积公式即可得出结论;
②因为只要MN=h=20,P在直线b上任意位置时,△PMN的面积取得最大值,因为不能确定P点位置,所以∠PMN得大小无法确定,因此不能求出∠PMN的正切值;
(2)①作出△PMN,由图可知△PMN是以线段MN为底的等腰三角形;
②根据勾股定理求出PN的长,进而可得出结论;
(3)将△MPA绕点M顺时针旋转60°得到△MP′A′,根据图形旋转的性质得出P′A′=PA,∠MA′P′=120°.连接AA′,则△MAA′是等边三角形.由此可得出P′,A′,A,N四点在一条直线上,故AP+AM+AN=P′A′+AA′+AN=P′N,所以AP+AM+AN和的最小值等于P′N的长,由此可得出结论.
解答 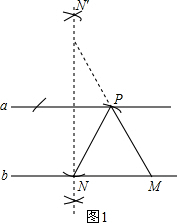 解:(1)①∵x+h=40,
解:(1)①∵x+h=40,
∴h=40-x,
S=$\frac{1}{2}$x(40-x)=-$\frac{1}{2}$x2+20x,
∵S=-$\frac{1}{2}$(x-20)2+200,
∴当MN=20时,△PMN的面积最大,最大面积为200;
②不能.
因为只要MN=h=20,P在直线b上任意位置时,△PMN的面积取得最大值,因为不能确定P点位置,所以∠PMN得大小无法确定,因此不能求出∠PMN的正切值;
(2)①如图1,△PMN是以线段MN为底的等腰三角形.
②周长最小时点P为MN的垂直平分线与直线a的交点;
(3)如图2,在等腰△PMN的顶角∠MPN的平分线上取点A,使得∠AMN=∠ANM=30°,点A在此处可使得AP+AM+AN的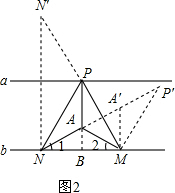 和最小.
和最小.
∵此时∠MAP=∠NAP=∠NAM=120°.
将△MPA绕点M顺时针旋转60°得到△MP′A′.
∴P′A′=PA,∠MA′P′=120°.
连接AA′,则△MAA′是等边三角形.
∴MA=AA′,∠MA′A=∠NAA′=60°.
∴∠MA′P+MAA′=MAA′+∠MAN=180°.
即P′,A′,A,N四点在一条直线上,
∴AP+AM+AN=P′A′+AA′+AN=P′N,
∴AP+AM+AN和的最小值等于P′N的长,
此时,NA=MA=10÷cos30°=$\frac{20\sqrt{3}}{3}$,AB=10×tan30°=$\frac{10\sqrt{3}}{3}$,
∴AP+AM+AN的最小值为:20-$\frac{10\sqrt{3}}{3}$+2×$\frac{20\sqrt{3}}{3}$=20+10$\sqrt{3}$.
点评 本题考查的是二次函数综合题,涉及到二次函数的最值问题,等腰三角形的判定与性质等知识,在解答(3)时涉及到图形的旋转及三角形函数的定义等知识,难度较大.

| A. | a3+a=2a4 | B. | a6÷a-3=a3 | C. | a3•a3=2a3 | D. | (-2a2)3=-8a6 |
| A. | x>-1 | B. | x>2 | C. | x<-1 | D. | x<2 |
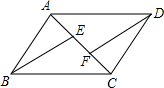 已知平行四边形ABCD中,BE∥DF,求证:AE=CF.
已知平行四边形ABCD中,BE∥DF,求证:AE=CF. 如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为18°,且OA=OB=3m.
如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为18°,且OA=OB=3m.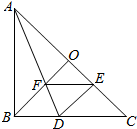 如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连结DE、EF.下列结论:①tan∠ADB=2;②图中有4对全等三角形;③BD=BF;④S四边形DFOE=S△AOF;⑤若将△DEF沿EF折叠,则点D一定落在AC上,上述结论中正确的个数是( )
如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连结DE、EF.下列结论:①tan∠ADB=2;②图中有4对全等三角形;③BD=BF;④S四边形DFOE=S△AOF;⑤若将△DEF沿EF折叠,则点D一定落在AC上,上述结论中正确的个数是( ) 如图,在△ABC中,AD是边BC上的中线,设向量$\overline{AB}$=$\overline{a}$,$\overline{AD}$=$\overline{b}$,如果用向量$\overline{a}$,$\overline{b}$表示向量$\overline{BC}$,那$\overline{BC}$=2$\overline{b}$-2$\overline{a}$.
如图,在△ABC中,AD是边BC上的中线,设向量$\overline{AB}$=$\overline{a}$,$\overline{AD}$=$\overline{b}$,如果用向量$\overline{a}$,$\overline{b}$表示向量$\overline{BC}$,那$\overline{BC}$=2$\overline{b}$-2$\overline{a}$.