题目内容
3.若关于x、y的二元一次方程组$\left\{{\begin{array}{l}{2x-y=n\;}\\{mx+3y=2}\end{array}}\right.$有无数个解,则m=-6、n=-$\frac{2}{3}$.分析 根据方程组有无数组解可知两方程未知数的系数成比例,据此可得出结论.
解答 解:∵关于x、y的二元一次方程组$\left\{{\begin{array}{l}{2x-y=n\;}\\{mx+3y=2}\end{array}}\right.$有无数个解,
∴$\frac{2}{m}$=$\frac{-1}{3}$=$\frac{n}{2}$,
解得m=-6,n=-$\frac{2}{3}$.
故答案为:=-6,=-$\frac{2}{3}$.
点评 本题考查的是二元一次方程组的解,熟知二元一次方程组有无数组解得条件是解答此题的关键.

练习册系列答案
相关题目
11.3.14-π的相反数为( )
| A. | 0 | B. | 3.14-π | C. | π-3.14 | D. | 0.14 |
18.下列四项有关数学成就的说法正确的是( )
| A. | 我国是最早使用负数的国家 | B. | 我国是最早使用圆周率π的国家 | ||
| C. | 我国是最早使用“×”(乘号)的国家 | D. | 我国是最早使用几何的国家 |
12.下列条件能让两个三角形全等的是( )
| A. | 有一边和两角对应相等 | B. | 有两边和一角对应相等 | ||
| C. | 三个角对应相等 | D. | 面积相等且有一边相等 |
 如图,在△ABC中,AB=AC=10cm,EF是边AB的垂直平分线,且△AEC的周长为24cm,则BC的长=14cm.
如图,在△ABC中,AB=AC=10cm,EF是边AB的垂直平分线,且△AEC的周长为24cm,则BC的长=14cm.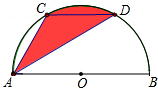 如图,已知AB为半圆O的直径,弦CD=8厘米,CD∥AB,∠CAD=30°,则图中阴影部分的面积等于$\frac{32π}{3}$平方厘米.
如图,已知AB为半圆O的直径,弦CD=8厘米,CD∥AB,∠CAD=30°,则图中阴影部分的面积等于$\frac{32π}{3}$平方厘米.