题目内容
9.计算:(1)2tan45°-sin60°cos45°
(2)$2sin{45°}+{2^{-1}}-\frac{1}{{1-tan{{30}°}}}+|2-\sqrt{2}|$.
分析 (1)首先代入特殊角的三角函数,然后计算求值即可;
(2)首先代入特殊角的三角函数,然后进行分母有理化,最后合并同类二次根式求解即可.
解答 解:(1)原式=2×1-$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{2}}{2}$=2-$\frac{\sqrt{6}}{4}$;
(2)原式=2×$\frac{\sqrt{2}}{2}$+$\frac{1}{2}$-$\frac{1}{1-\frac{\sqrt{3}}{3}}$+2-$\sqrt{2}$
=$\sqrt{2}$+$\frac{1}{2}$-$\frac{3}{3-\sqrt{3}}$+2-$\sqrt{2}$
=$\sqrt{2}$+$\frac{1}{2}$-$\frac{1}{2}$(3+$\sqrt{3}$)+2-$\sqrt{2}$
=$\sqrt{2}$+$\frac{1}{2}$-$\frac{3}{2}$-$\frac{\sqrt{3}}{2}$+2-$\sqrt{2}$
=1-$\frac{\sqrt{3}}{2}$.
点评 本题考查的是二次根式的混合运算以及特殊角的三角函数值,正确对二次根式进行分母有理化是本题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
19.下列事件中:①在足球赛中,中国队战胜日本队;②长为2,3,4的三条线段能围成一个直角三角形;③任意两个正数的乘积为正;④抛一枚硬币,硬币落地时正面朝上.其中属于不确定事件的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.$\sqrt{{{({3.14-π})}^2}}-\sqrt{{{({π-3.14})}^2}_{\;}}$的值是( )
| A. | -2π | B. | 6.28 | C. | 0 | D. | 6.28-2π |
 画出下面几何体从正面、左面、上面看到的图形.
画出下面几何体从正面、左面、上面看到的图形.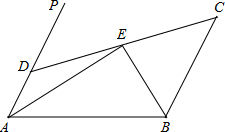 如图,AD∥BC,∠PAB的平分线交于E,CE的延长线交AP于D,求证:AD+BC=AB.
如图,AD∥BC,∠PAB的平分线交于E,CE的延长线交AP于D,求证:AD+BC=AB.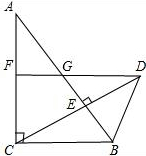 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB交AB于点E,且CD=AC,DF∥BC,分别与AB,AC交于点G,F(说明:在有一个锐角为30°的直角三角形中,30°角所对的直角边长是斜边长的一半.)
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB交AB于点E,且CD=AC,DF∥BC,分别与AB,AC交于点G,F(说明:在有一个锐角为30°的直角三角形中,30°角所对的直角边长是斜边长的一半.) 求阴影部分的周长和面积(单位:cm).
求阴影部分的周长和面积(单位:cm).