题目内容

5．（1）①35a7b3c÷7a4bc5a3b2；②-3x•（2x2-x+4）=-6x3+3x2-12x；
（2）已知$a-\frac{1}{a}=3$，则${a^2}+\frac{1}{a^2}$的值等于11．
（3）因式分解：2am2-8a=2a（m+2）（m-2）．

分析 （1）①原式利用单项式除以单项式法则计算即可得到结果；②原式利用单项式乘以多项式法则计算即可得到结果；
（2）原式利用完全平方公式变形，将已知等式代入计算即可求出值；
（3）原式提取2a，再利用平方差公式分解即可．

解答 解：（1）①原式=5a3b2；②-6x3+3x2-12x；
（2）∵a-$\frac{1}{a}$=3，
∴原式=（a-$\frac{1}{a}$）2+2=9+2=11；
（3）原式=2a（m2-4）=2a（m+2）（m-2），
故答案为：（1）①原式=5a3b2；②-6x3+3x2-12x；（2）11；（3）2a（m+2）（m-2），

点评 此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
2．如图，点E为正方形ABCD的边BC所在直线上的一点，连接AE，过点C作CF⊥AE于F，连接BF．
（1）如图1，当点E在CB的延长线上，且AC=EC时，求证：BF=$\frac{1}{2}AE$；
（2）如图2，当点E在线段BC上，且AE平分∠BAC时，求证：AB+BE=AC；
（3）如图3，当点E继续往右运动到BC中点时，过点D作DH⊥AE于H，连接BH．求证：∠BHF=45°．
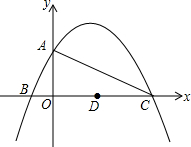16．如图，已知二次函数y=-$\frac{1}{4}$x2+$\frac{3}{2}x$+4的图象与y轴交于点A，与x轴交于B、C两点，其对称轴与x轴交于点D，连接AC．
（1）点A的坐标为（0，4），点C的坐标为（8，0）；
（2）将△AOC绕点D顺时针旋转90°得△PMN，A点对应的点为P点，判断点P是否在该抛物线上；
（3）在抛物线上是否存在点E，使得△EDC的面积为△OAC面积的$\frac{5}{8}$？若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由．
13．用规定的方法解方程
（1）2x2-7x+1=0（配方法）
（2）x2-$\frac{12}{{x}^{2}-2x}$=2x-1（换元法）
20．$\sqrt{{{（{3.14-π}）}^2}}-\sqrt{{{（{π-3.14}）}^2}_{\;}}$的值是（　　）
A．-2πB．6.28C．0D．6.28-2π
10．计算：
（1）22-（-4）
（2）-8÷（-2）+4×（-5）
（3）-24×（-$\frac{1}{2}$+$\frac{3}{4}$-$\frac{1}{3}$）
（4）-14÷（-5）2×（-$\frac{5}{3}$）+|0.8-1|
17．比大小：
-0.3＞-$\frac{1}{3}$；
|-4+5|＜|-4|+|-5|．
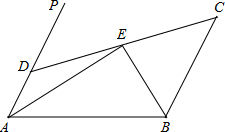14．如图，AD∥BC，∠PAB的平分线交于E，CE的延长线交AP于D，求证：AD+BC=AB．
15．用总长30m的篱笆沿墙的一边围一个长方形鸡舍，除墙这一边外，其他三边（门除外）都用篱笆围成，要求长方形的长是宽的2倍，并要求在墙的对边留2m宽的门，这个长方形的鸡舍的长与宽分别为16m，8m．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网