题目内容
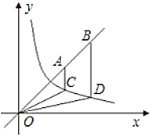
【题目】如图，点
，
为直线
上的两点，过，两点分别作
轴的平行线交双曲线
（
）于
、
两点.若
，则
的值为（ ）
A.12B.7C.6D.4
【答案】C
【解析】
延长AC交x轴于E，延长BD交x轴于F．设A、B的横坐标分别是a，b，点A、B为直线y=x上的两点，A的坐标是(a，a)，B的坐标是(b，b)．则AE=OE=a，BF=OF=b．根据BD=2AC即可得到a，b的关系，然后利用勾股定理，即可用a，b表示出所求的式子从而求解．
延长AC交x轴于E，延长BD交x轴于F．
设A、B的横坐标分别是a，b．
∵点A、B为直线y=x上的两点，
∴A的坐标是(a，a)，B的坐标是(b，b)．则AE=OE=a，BF=OF=b．
∵C、D两点在交双曲线
(x＞0)上，则CE
，DF
，
∴BD=BF﹣DF=b
，AC=a
．
又∵BD=2AC，
∴b
2(a)，
两边平方得：b2
2=4(a2
2)，即b2
4(a2
)﹣6．
在直角△OCE中，OC2=OE2+CE2=a2，同理OD2=b2
，
∴4OC2﹣OD2=4(a2)﹣(b2)=6．
故选：C．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
【题目】在初中阶段的函数学习中，我们经历了“确定函数的表达式——利用函数图象研其性质——运用函数解决问题”的学习过程．如图，在平面直角坐标系中己经绘制了一条直线
．另一函数
与
的函数关系如下表：
| … | －6 | －5 | －4 | －3 | －2 | －1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| … | －2 | －0.25 | 1 | 1.75 | 2 | 1.75 | 1 | －0.25 | －2 | －4.25 | －7 | －10.25 | －14 | … |
（1）求直线的解析式；
（2）请根据列表中的数据，绘制出函数的近似图像；
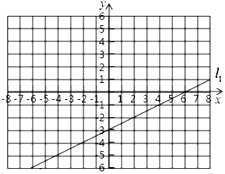
（3）请根据所学知识并结合上述信息拟合出函数的解折式，并求出与的交点坐标．
