题目内容
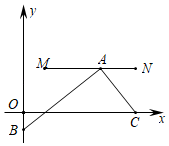
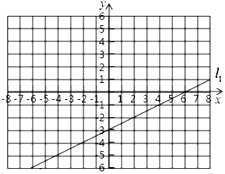
【题目】在初中阶段的函数学习中，我们经历了“确定函数的表达式——利用函数图象研其性质——运用函数解决问题”的学习过程．如图，在平面直角坐标系中己经绘制了一条直线
．另一函数
与
的函数关系如下表：
| … | －6 | －5 | －4 | －3 | －2 | －1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| … | －2 | －0.25 | 1 | 1.75 | 2 | 1.75 | 1 | －0.25 | －2 | －4.25 | －7 | －10.25 | －14 | … |
（1）求直线的解析式；
（2）请根据列表中的数据，绘制出函数的近似图像；
（3）请根据所学知识并结合上述信息拟合出函数的解折式，并求出与的交点坐标．
【答案】（1）
；（2）见解析；（3）交点为
和
【解析】
（1）根据待定系数法即可求出直线
的解析式；
（2）描点连线即可；
（3）根据图象得出函数为二次函数，顶点坐标为(-2，2)，用待定系数法即可求出抛物线的解析式，解方程组即可得出
与交点坐标．
（1）设直线的解析式为y=kx+m．
由图象可知，直线过点(6，0)，(0，-3)，
∴
，
解得：
，
∴；
（2）图象如图：
（3）由图象可知：函数为抛物线，顶点为
．
设其解析式为：
从表中选一点
代入得：
1=4a+2，
解出：
，
∴
，
即
．
联立两个解析式：
，
解得：
或
，
∴交点为和．
练习册系列答案
相关题目
【题目】在一次数学测试中，同年级人数相同的甲、乙两个班的成绩统计如下表：
班级 | 平均分 | 中位数 | 方差 |
甲班 |
|
|
|
乙班 |
|
|
|
数学老师让同学们针对统计的结果进行一下评估，学生的评估结果如下：
这次数学测试成绩中，甲、乙两个班的平均水平相同；
甲班学生中数学成绩95分及以上的人数少；
乙班学生的数学成绩比较整齐，分化较小．
上述评估中，正确的是______
填序号
