题目内容
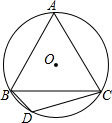 如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5
如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5| 2 |
考点:正多边形和圆
专题:
分析:首先连接OB,OC,OD,由等边△ABC内接于⊙O,BD为内接正十二边形的一边,可求得∠BOC,∠BOD的度数,继而证得△COD是等腰直角三角形,继而求得答案.
解答: 解:连接OB,OC,OD,
解:连接OB,OC,OD,
∵等边△ABC内接于⊙O,BD为内接正十二边形的一边,
∴∠BOC=
×360°=120°,∠BOD=
×360°=30°,
∴∠COD=∠BOC-∠BOD=90°,
∵OC=OD,
∴∠OCD=45°,
∴OC=CD•cos45°=5
×
=5(cm).
即⊙O的半径R=5cm.
 解:连接OB,OC,OD,
解:连接OB,OC,OD,∵等边△ABC内接于⊙O,BD为内接正十二边形的一边,
∴∠BOC=
| 1 |
| 3 |
| 1 |
| 12 |
∴∠COD=∠BOC-∠BOD=90°,
∵OC=OD,
∴∠OCD=45°,
∴OC=CD•cos45°=5
| 2 |
| ||
| 2 |
即⊙O的半径R=5cm.
点评:此题考查了正多边形与圆以及等腰直角三角形性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
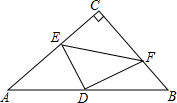 如图,将直角三角形纸片ABC折叠,使直角顶点C落在斜边中点D的位置,EF是折痕,已知DE=15,DF=20,求AB的长.
如图,将直角三角形纸片ABC折叠,使直角顶点C落在斜边中点D的位置,EF是折痕,已知DE=15,DF=20,求AB的长.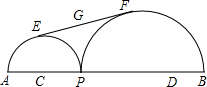 已知线段AB=6,C、D是AB上两点,且AC=DB=1,P是线段CD上一动点,在AB同侧分别以AP和BP为直径作半圆,点E,F分别为以AP和BP为直径所作半圆的弧的中点,连接EF,点G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为
已知线段AB=6,C、D是AB上两点,且AC=DB=1,P是线段CD上一动点,在AB同侧分别以AP和BP为直径作半圆,点E,F分别为以AP和BP为直径所作半圆的弧的中点,连接EF,点G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为 如图,正方形ABCD的边长为
如图,正方形ABCD的边长为