题目内容
已知一个圆锥的表面积为340π,底面圆的周长为20π,求这个圆锥侧面展开图的圆心角.
考点:圆锥的计算
专题:
分析:先根据圆的周长公式求出圆锥的底面半径r=10,那么圆锥的底面积为:π×102=100π,根据圆锥的表面积=底面积+侧面积,得到圆锥的侧面积为:340π-100π=240π,再由S侧=πrl求出圆锥的母线长l=24,然后根据弧长计算公式即可求解.
解答:解:设圆锥的底面半径是r,则2πr=20π,
解得:r=10,
圆锥的底面积为:π×102=100π,
侧面积为:340π-100π=240π,
设圆锥的母线长为l,则π×10l=240π,
解得l=24.
设这个圆锥侧面展开图的圆心角为n°,则
=20π,
解得n=150,
即这个圆锥侧面展开图的圆心角为150°.
解得:r=10,
圆锥的底面积为:π×102=100π,
侧面积为:340π-100π=240π,
设圆锥的母线长为l,则π×10l=240π,
解得l=24.
设这个圆锥侧面展开图的圆心角为n°,则
| nπ×24 |
| 180 |
解得n=150,
即这个圆锥侧面展开图的圆心角为150°.
点评:本题考查扇形与圆锥的相关计算.解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.

练习册系列答案
相关题目
 如图,?ABCD中,∠DAB的平分线交CD于点E,AE的中点是H,经过点E作AE的垂线交BC于G,交AB的延长线于点F,点G恰好是EF的中点,DH=GC.
如图,?ABCD中,∠DAB的平分线交CD于点E,AE的中点是H,经过点E作AE的垂线交BC于G,交AB的延长线于点F,点G恰好是EF的中点,DH=GC.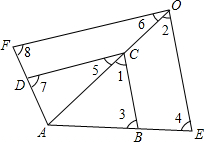 如图,已知△AEO∽△ABC,△AOF∽△ACD,那么四边形ABCD与四边形AEOF相似吗?请说明你的理由.
如图,已知△AEO∽△ABC,△AOF∽△ACD,那么四边形ABCD与四边形AEOF相似吗?请说明你的理由.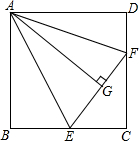 如图正方形ABCD的边长为8cm,E是BC边的中点.把△ABE沿AE折叠到△AGE的位置,F是CD边上的一点,把△ADF沿AF折叠,D点恰好落在G点上,求CF的长度.
如图正方形ABCD的边长为8cm,E是BC边的中点.把△ABE沿AE折叠到△AGE的位置,F是CD边上的一点,把△ADF沿AF折叠,D点恰好落在G点上,求CF的长度.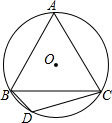 如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5
如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5 如图,△ABC内接于⊙O,且AC=AB,点D在
如图,△ABC内接于⊙O,且AC=AB,点D在
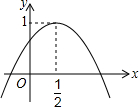 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点的坐标为(
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点的坐标为(