题目内容
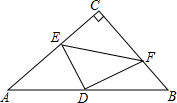 如图,将直角三角形纸片ABC折叠,使直角顶点C落在斜边中点D的位置,EF是折痕,已知DE=15,DF=20,求AB的长.
如图,将直角三角形纸片ABC折叠,使直角顶点C落在斜边中点D的位置,EF是折痕,已知DE=15,DF=20,求AB的长.考点:翻折变换(折叠问题)
专题:
分析:利用勾股定理得出EF的长,再利用三角形面积得出
CD的长,进而得出答案.
| 1 |
| 2 |
解答: 解:连接CD,
解:连接CD,
因为折叠,△CEF的位置到达△DEF,△CEF是直角三角形,
∴CE=DE=15,
CF=DF=20,
由勾股定理得:EF=25,
∵∠EDF=∠C=90°,且CD⊥EF,CD被平分,
∴
CD=EC×CF÷EF=15×20÷25=12,
∴CD=24,
∵CD是AB的中线,
∴AB=2CD=2×24=48(直角三角形斜边上的中线等于斜边的一半).
 解:连接CD,
解:连接CD,因为折叠,△CEF的位置到达△DEF,△CEF是直角三角形,
∴CE=DE=15,
CF=DF=20,
由勾股定理得:EF=25,
∵∠EDF=∠C=90°,且CD⊥EF,CD被平分,
∴
| 1 |
| 2 |
∴CD=24,
∵CD是AB的中线,
∴AB=2CD=2×24=48(直角三角形斜边上的中线等于斜边的一半).
点评:此题主要考查了翻折变换的性质以及勾股定理,得出
CD的长是解题关键.
| 1 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
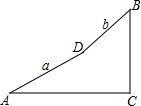 如图:BC⊥AC,设AD=a,DB=b,∠A=α,∠B=β,则用含a、b、α、β的式子表示AC正确的为( )
如图:BC⊥AC,设AD=a,DB=b,∠A=α,∠B=β,则用含a、b、α、β的式子表示AC正确的为( )| A、asinα+bsinβ |
| B、asinα+bcosβ |
| C、acosα+bsinβ |
| D、acosα+bcosβ |
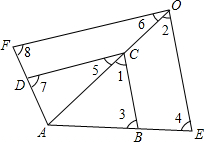 如图,已知△AEO∽△ABC,△AOF∽△ACD,那么四边形ABCD与四边形AEOF相似吗?请说明你的理由.
如图,已知△AEO∽△ABC,△AOF∽△ACD,那么四边形ABCD与四边形AEOF相似吗?请说明你的理由.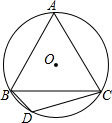 如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5
如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5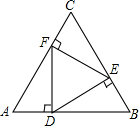 如图,△ABC是等边三角形,点D,E,F分别在边AB,BC,CA上,且DE⊥BC,EF⊥AC,FD⊥AB.若△ABC的面积为72cm2,求△DEF的面积.
如图,△ABC是等边三角形,点D,E,F分别在边AB,BC,CA上,且DE⊥BC,EF⊥AC,FD⊥AB.若△ABC的面积为72cm2,求△DEF的面积.