题目内容
7.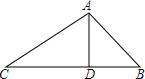 先阅读材料.再解答下面的问题:问题:在△ABC中,AD是边BC上的高,AD=2,DB=2,CD=2$\sqrt{3}$,求∠BAC的度数.
先阅读材料.再解答下面的问题:问题:在△ABC中,AD是边BC上的高,AD=2,DB=2,CD=2$\sqrt{3}$,求∠BAC的度数.王刚是这样解答的:
如图.在Rt△ACD中,tan∠CAD=$\frac{CD}{AD}$=$\sqrt{3}$,则∠CAD=60°.在Rt△ADB中,tan∠BAD=$\frac{BD}{AD}$=1,则∠BAD=45°.
∴∠BAC=∠CAD+∠BAD=105°.你认为王刚的解法正确吗?为什么?如果不正确.请指出错误之处.并写出正确的答案.
分析 根据在直角三角形中,一个锐角的正切等于这个角对边比这个角的邻边即可得到结论.
解答 解:王刚的解法正确,
理由:根据正切函数的定义,当α为锐角,则tanα=$\frac{α的对边}{α的邻边}$,
故王刚的解法正确.
点评 本题考查了解直角三角形,三角函数的定义,熟记三角函数的定义是解题的关键.

练习册系列答案
相关题目
12.多项式的乘法法则知:若(x+a)(x+b)=x2+px+q,则p=a+b,q=a•b;反过来x2+px+q=(x+a)(x+b),要将多项式x2+px+q进行分解,关键是找到两个数a、b,使a+b=p,a•b=q,如对多项式x2-3x+2,有p=-3,q=2,a=-1,b=-2,此时(-1)+(-2)=-3,(-1)(-2)=2,所以x2-3x+2可分解为(x-1)(x-2),即x2-3x+2=(x-1)(x-2)
(1)根据以上填写下表:
(2)根据填表,还可得出如下结论:当q是正数时,应分解成两个因数a、b同号,a、b的符号与p相同;当q为负数时,应分解成的两个因数a、b异号,a、b中绝对值较大的因数的符合与p相同.
(3)分解因式x2-x-12=(x-4)(x+3);x2-7x+6=(x-1)(x-6).
(1)根据以上填写下表:
| 多项式 | p | q | a | b | 分解结果 |
| x2+9x+20 | 9 | 20 | 4 | 5 | (x+4)(x+5) |
| x2-9x+20 | -9 | 20 | -4 | -5 | (x-4)(x-5) |
(3)分解因式x2-x-12=(x-4)(x+3);x2-7x+6=(x-1)(x-6).
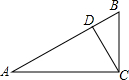 如图,△ABC中,∠ACB=90°,BC=8,AC=12,∠BCD=30°,求线段CD长.
如图,△ABC中,∠ACB=90°,BC=8,AC=12,∠BCD=30°,求线段CD长.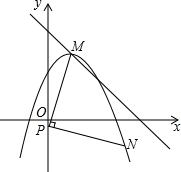 已知,抛物线y=-$\frac{3}{4}$(x-1)2+3顶点为M,点N在抛物线,点P在y轴上,(点M、N、P逆时针方向排列),PN=PM,PN⊥PM,求P点坐标.
已知,抛物线y=-$\frac{3}{4}$(x-1)2+3顶点为M,点N在抛物线,点P在y轴上,(点M、N、P逆时针方向排列),PN=PM,PN⊥PM,求P点坐标.