题目内容
19. 如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.
如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.(1)求证:∠BME=∠MAB;
(2)如果BE=$\frac{18}{5}$,sin∠BAM=$\frac{3}{5}$,求⊙O的半径.
分析 (1)由切线的性质得出∠BME+∠OMB=90°,再由直径得出∠AMB=90°,利用同角的余角相等判断出结论;
(2)先在Rt△BEM中,用三角函数求出BM,再在Rt△ABM中,用三角函数和勾股定理计算即可.
解答 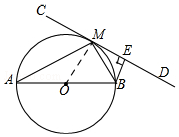 (1)如图,连接OM.
(1)如图,连接OM.
∵直线CD切⊙O于点M.
∴∠OMD=90°.
∴∠BME+∠OMB=90°.
∵AB为⊙O的直径.
∴∠AMB=90°.
∴∠AMO+∠OMB=90°.
∴∠BME=∠AMO.
∵OA=OM.
∴∠MAB=∠AMO.
∴∠BME=∠MAB;
(2)由(1)可得,∠BME=∠MAB.
∵sin∠BAM=$\frac{3}{5}$,
∴sin∠BME=$\frac{3}{5}$
在Rt△BEM中,BE=$\frac{18}{5}$.
∴sin∠BME=$\frac{BE}{BM}$=$\frac{3}{5}$.
∴BM=6,在Rt△ABM中,sin∠BAM=$\frac{3}{5}$.
∴sin∠BAM=$\frac{BM}{AB}$=$\frac{3}{5}$.
∴AB=$\frac{3}{5}$BM=10.
∴⊙O的半径=5
点评 本题主要考查了切线的性质,直径所对的圆周角是直径,相似三角形的性质和判定,三角函数,作出恰当的辅助线是解答此题的关键.

练习册系列答案
相关题目
14.农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润-日支出费用)
| 销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
| 日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润-日支出费用)
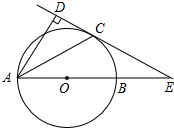 如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.
如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.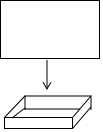 工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)
工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)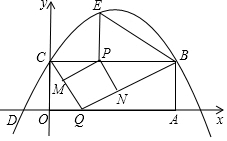 如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(-2,0),点P是线段CB上的动点,设CP=t(0<t<10).
如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(-2,0),点P是线段CB上的动点,设CP=t(0<t<10).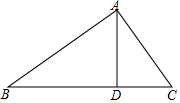 如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC的平分线,分别交AD,AC于P,Q两点;并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)
如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC的平分线,分别交AD,AC于P,Q两点;并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)