题目内容
14.农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:| 销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
| 日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润-日支出费用)
分析 (1)首先根据表中的数据,可猜想y与x是一次函数关系,任选两点求表达式,再验证猜想的正确性;
(2)根据题意列出日销售利润w与销售价格x之间的函数关系式,根据二次函数的性质确定最大值即可;
(3)根据题意列出日销售利润w与销售价格x之间的函数关系式,并求得抛物线的对称轴,再分两种情况进行讨论,依据二次函数的性质求得a的值.
解答 解:(1)假设p与x成一次函数关系,设函数关系式为p=kx+b,
则$\left\{\begin{array}{l}{30k+b=600}\\{40k+b=300}\end{array}\right.$,
解得:k=-30,b=1500,
∴p=-30x+1500,
检验:当x=35,p=450;当x=45,p=150;当x=50,p=0,符合一次函数解析式,
∴所求的函数关系为p=-30x+1500;
(2)设日销售利润w=p(x-30)=(-30x+1500)(x-30)
即w=-30x2+2400x-45000,
∴当x=-$\frac{2400}{2×(-30)}$=40时,w有最大值3000元,
故这批农产品的销售价格定为40元,才能使日销售利润最大;
(3)日获利w=p(x-30-a)=(-30x+1500)(x-30-a),
即w=-30x2+(2400+30a)x-(1500a+45000),
对称轴为x=-$\frac{2400+30a}{2×(-30)}$=40+$\frac{1}{2}$a,
①若a>10,则当x=45时,w有最大值,
即w=2250-150a<2430(不合题意);
②若a<10,则当x=40+$\frac{1}{2}$a时,w有最大值,
将x=40+$\frac{1}{2}$a代入,可得w=30($\frac{1}{4}$a2-10a+100),
当w=2430时,2430=30($\frac{1}{4}$a2-10a+100),
解得a1=2,a2=38(舍去),
综上所述,a的值为2.
点评 本题主要考查了二次函数的综合应用,解题时要利用图表中的信息,学会用待定系数法求解函数解析式,并将实际问题转化为求函数最值问题,从而来解决实际问题.

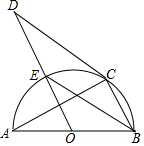 如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( )
如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( )| A. | AC⊥BC | B. | BE平分∠ABC | C. | BE∥CD | D. | ∠D=∠A |
| x(元/件) | 10 | 12 | 14 | 16 |
| y(件) | 200 | 180 | 160 | 140 |
(2)为使商场每周获得最大利润,试问这种背心定价应为多少?最大利利润是多少?
(3)若商场每周想要获得不低于1050元的利润,试确定这种儿童背心的定价x(元/件)的取值范围.
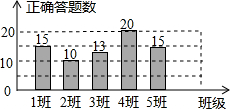 某校举行“汉字听写比赛”,5个班级代表队的正确答题数如图.这5个正确答题数所组成的一组数据的中位数和众数分别是( )
某校举行“汉字听写比赛”,5个班级代表队的正确答题数如图.这5个正确答题数所组成的一组数据的中位数和众数分别是( )| A. | 10,15 | B. | 13,15 | C. | 13,20 | D. | 15,15 |
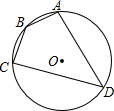 如图,四边形ABCD内接于⊙O,⊙O的半径为3,∠B=140°,则弧AC的长为$\frac{4}{3}$π.
如图,四边形ABCD内接于⊙O,⊙O的半径为3,∠B=140°,则弧AC的长为$\frac{4}{3}$π. 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点D的坐标为($\sqrt{5}$,2).
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点D的坐标为($\sqrt{5}$,2). 如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.
如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.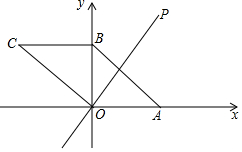 如图,在平面直角坐标系xOy中,?ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线y=$\frac{3}{2}$x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与?ABCO的边相切时,P点的坐标为(0,0)或($\frac{2}{3}$,1)或(3-$\sqrt{5}$,$\frac{9-3\sqrt{5}}{2}$).
如图,在平面直角坐标系xOy中,?ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线y=$\frac{3}{2}$x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与?ABCO的边相切时,P点的坐标为(0,0)或($\frac{2}{3}$,1)或(3-$\sqrt{5}$,$\frac{9-3\sqrt{5}}{2}$).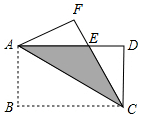 如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.