题目内容
9.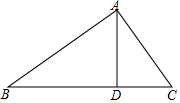 如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC的平分线,分别交AD,AC于P,Q两点;并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)
如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC的平分线,分别交AD,AC于P,Q两点;并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)
分析 根据角平分线的性质作出BQ即可.先根据垂直的定义得出∠ADB=90°,故∠BPD+∠PBD=90°.
再根据余角的定义得出∠AQP+∠ABQ=90°,根据角平分线的性质得出∠ABQ=∠PBD,再由∠BPD=∠APQ可知∠APQ=∠AQP,据此可得出结论.
解答  解:BQ就是所求的∠ABC的平分线,P、Q就是所求作的点.
解:BQ就是所求的∠ABC的平分线,P、Q就是所求作的点.
证明:∵AD⊥BC,
∴∠ADB=90°,
∴∠BPD+∠PBD=90°.
∵∠BAC=90°,
∴∠AQP+∠ABQ=90°.
∵∠ABQ=∠PBD,
∴∠BPD=∠AQP.
∵∠BPD=∠APQ,
∴∠APQ=∠AQP,
∴AP=AQ.
点评 本题考查的是作图-基本作图,熟知角平分线的作法和性质是解答此题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
20.若x与3互为相反数,则|x+3|等于( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
4.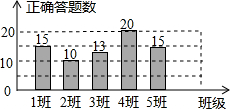 某校举行“汉字听写比赛”,5个班级代表队的正确答题数如图.这5个正确答题数所组成的一组数据的中位数和众数分别是( )
某校举行“汉字听写比赛”,5个班级代表队的正确答题数如图.这5个正确答题数所组成的一组数据的中位数和众数分别是( )
 某校举行“汉字听写比赛”,5个班级代表队的正确答题数如图.这5个正确答题数所组成的一组数据的中位数和众数分别是( )
某校举行“汉字听写比赛”,5个班级代表队的正确答题数如图.这5个正确答题数所组成的一组数据的中位数和众数分别是( )| A. | 10,15 | B. | 13,15 | C. | 13,20 | D. | 15,15 |
1.大米包装袋上(10±0.1)kg的标识表示此袋大米重( )
| A. | (9.9~10.1)kg | B. | 10.1kg | C. | 9.9kg | D. | 10kg |
18.若正多边形的一个内角是150°,则该正多边形的边数是( )
| A. | 6 | B. | 12 | C. | 16 | D. | 18 |
 如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.
如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.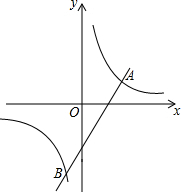 如图,一次函数y=2x-4的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且点A的横坐标为3.
如图,一次函数y=2x-4的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且点A的横坐标为3. 如图,⊙O的半径为2,点A,B在⊙O上,∠AOB=90°,则阴影部分的面积为π-2.
如图,⊙O的半径为2,点A,B在⊙O上,∠AOB=90°,则阴影部分的面积为π-2.