题目内容
4.设点(-1,m)和点($\frac{1}{2}$,n)是直线y=(k2-1)x+b(0<k<1)上的两个点,则m、n的大小关系为m>n.分析 先根据一次函数的解析式判断出该函数的增减性,再根据-1<$\frac{1}{2}$及可判断出m、n的大小.
解答 解:∵0<k<1,
∴直线y=(k2-1)x+b中,k2-1<0,
∴y随x的增大而减小,
∵-1<$\frac{1}{2}$,
∴m>n.
故答案是:m>n.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数的增减性是解答此题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1,、…、正方形AnBnCnCn-1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则△A2017A2018B2017的面积是24031.
在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1,、…、正方形AnBnCnCn-1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则△A2017A2018B2017的面积是24031. 如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.
如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.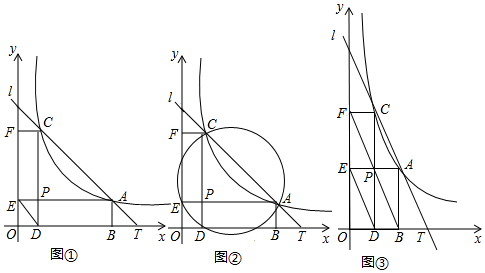
 如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3.
如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3. 如图,⊙O的半径为2,点A,B在⊙O上,∠AOB=90°,则阴影部分的面积为π-2.
如图,⊙O的半径为2,点A,B在⊙O上,∠AOB=90°,则阴影部分的面积为π-2.