题目内容
已知关于x的方程x2-(2k-3)x+k2+1=0有两个不相等的实数根x1、x2.
(1)求k的取值范围;
(2)试说明x1<0,x2<0;
(3)若抛物线y=x2-(2k-3)x+k2+1与x轴交于A、B两点,点A、点B到原点的距离分别为OA、OB,且OA+OB=2OA•OB-3,求k的值.
(1)求k的取值范围;
(2)试说明x1<0,x2<0;
(3)若抛物线y=x2-(2k-3)x+k2+1与x轴交于A、B两点,点A、点B到原点的距离分别为OA、OB,且OA+OB=2OA•OB-3,求k的值.
考点:抛物线与x轴的交点,根的判别式,根与系数的关系
专题:代数综合题
分析:(1)方程有两个不相等的实数根,则判别式大于0,据此即可列不等式求得k的范围;
(2)利用根与系数的关系,说明两根的和小于0,且两根的积大于0即可;
(3)不妨设A(x1,0),B(x2,0).利用x1,x2表示出OA、OB的长,则根据根与系数的关系,以及OA+OB=2OA•OB-3即可列方程求解.
(2)利用根与系数的关系,说明两根的和小于0,且两根的积大于0即可;
(3)不妨设A(x1,0),B(x2,0).利用x1,x2表示出OA、OB的长,则根据根与系数的关系,以及OA+OB=2OA•OB-3即可列方程求解.
解答:解:(1)由题意可知:△=[-(2k-3)]2-4(k2+1)>0,
即-12k+5>0
∴k<
.
(2)∵
,
∴x1<0,x2<0.
(3)依题意,不妨设A(x1,0),B(x2,0).
∴OA+OB=|x1|+|x2|=-(x1+x2)=-(2k-3),
OA•OB=|-x1||x2|=x1x2=k2+1,
∵OA+OB=2OA•OB-3,
∴-(2k-3)=2(k2+1)-3,
解得k1=1,k2=-2.
∵k<
,
∴k=-2.
即-12k+5>0
∴k<
| 5 |
| 12 |
(2)∵
|
∴x1<0,x2<0.
(3)依题意,不妨设A(x1,0),B(x2,0).
∴OA+OB=|x1|+|x2|=-(x1+x2)=-(2k-3),
OA•OB=|-x1||x2|=x1x2=k2+1,
∵OA+OB=2OA•OB-3,
∴-(2k-3)=2(k2+1)-3,
解得k1=1,k2=-2.
∵k<
| 5 |
| 12 |
∴k=-2.
点评:本题考查了二次函数与x轴的交点,两交点的横坐标就是另y=0,得到的方程的两根,则满足一元二次方程的根与系数的关系.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 如图是三种不同类型的地砖,若现有A类4块,B类2块,C类1块,若要拼成一个正方形到还需B类地砖
如图是三种不同类型的地砖,若现有A类4块,B类2块,C类1块,若要拼成一个正方形到还需B类地砖 图1中的中国结挂件是由四个相同的菱形在顶点处依次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.
图1中的中国结挂件是由四个相同的菱形在顶点处依次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.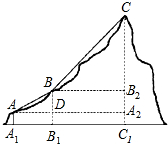 如图,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AA1,BB1,CC1分别为160米,400米,1000米,钢缆AB,BC分别与水平线AA2,BB2所成的夹角为30°,45°,求钢缆AB和BC的总长度.(结果精确到1米)
如图,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AA1,BB1,CC1分别为160米,400米,1000米,钢缆AB,BC分别与水平线AA2,BB2所成的夹角为30°,45°,求钢缆AB和BC的总长度.(结果精确到1米) 如图,将一个长小形铁皮剪去一个小正方形.
如图,将一个长小形铁皮剪去一个小正方形. 如图,一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在OP上滑动,将窗户OM按图示方向向内旋转35°到达ON位置,此时,点A、C的对应位置分别是点B、D.测量出∠ODB为25°,点D到点O的距离为30cm.
如图,一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在OP上滑动,将窗户OM按图示方向向内旋转35°到达ON位置,此时,点A、C的对应位置分别是点B、D.测量出∠ODB为25°,点D到点O的距离为30cm.