题目内容
 如图是三种不同类型的地砖,若现有A类4块,B类2块,C类1块,若要拼成一个正方形到还需B类地砖
如图是三种不同类型的地砖,若现有A类4块,B类2块,C类1块,若要拼成一个正方形到还需B类地砖考点:多项式乘多项式
专题:
分析:分别计算出4块A的面积和2块B的面积、1块C的面积,再计算这三种类型的砖的总面积,用完全平方公式化简后,即可得出少了哪种类型的地砖.
解答:解:4块A的面积为:4×m×m=4m2;
2块B的面积为:2×m×n=2mn;
1块C的面积为n×n=n2;
那么这三种类型的砖的总面积应该是:
4m2+2mn+n2=4m2+4mn+n2-2mn=(2m+n)2-2mn,
因此,少2块B型地砖,
故答案为:2.
2块B的面积为:2×m×n=2mn;
1块C的面积为n×n=n2;
那么这三种类型的砖的总面积应该是:
4m2+2mn+n2=4m2+4mn+n2-2mn=(2m+n)2-2mn,
因此,少2块B型地砖,
故答案为:2.
点评:本题考查了完全平方公式的几何意义,立意较新颖,注意面积的不同求解是解题的关键,对此类问题要深入理解.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知a>b,c为任意实数,则下列不等式中总是成立的是( )
| A、a+c<b+c |
| B、a-c>b-c |
| C、ac<bc |
| D、ac>bc |
 如图,在Rt△ABC中,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则∠DCE的大小为
如图,在Rt△ABC中,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则∠DCE的大小为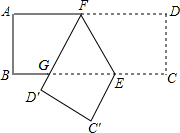 如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为
如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为