题目内容
12.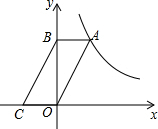 如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,过点A作AB∥x轴交y轴于点B,连结OA,过点B作BC∥OA交x轴于点C,若△BOC的面积是2,则k=4.
如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,过点A作AB∥x轴交y轴于点B,连结OA,过点B作BC∥OA交x轴于点C,若△BOC的面积是2,则k=4.
分析 根据题意四边形ABCO是平行四边形,求出△ABO的面积,利用公式:S△ABO=$\frac{|k|}{2}$即可解决问题.
解答 解:∵AO∥BC、AB∥CO,
∴四边形ABCO是平行四边形,
∴AO=BC,AB=CO,S△AOB=S△BOC=2,
∴$\frac{|k|}{2}=2$,
∵k>0,
∴k=4,
故答案为4.
点评 本题考查反比例函数系数k的几何意义,记住公式:S△ABO=$\frac{|k|}{2}$是解决问题的关键,属于中考常考题型.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
3.下列式子正确的是( )
| A. | 3a2b+2ab2=5a3b3 | B. | 2-$\frac{2}{x-1}$=$\frac{2x-4}{x-1}$ | C. | (x-2)(-x+2)=x2-4 | D. | a2•a3+a6=2a6 |
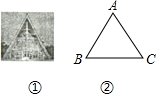 如图,某“A”字型监周屋如图①所示,房屋正面的平面图如图②所示,测得∠B=∠C=62°,BC=10.22米,求屋顶A到地面BC的距离(结果精确到0.1米)
如图,某“A”字型监周屋如图①所示,房屋正面的平面图如图②所示,测得∠B=∠C=62°,BC=10.22米,求屋顶A到地面BC的距离(结果精确到0.1米)


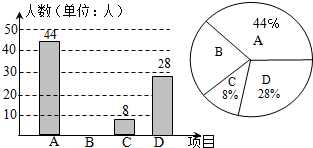

 如图,⊙O是Rt△ABC的内切圆,∠C=90°,BO的延长线交AC于点D,若BC=4,CD=2,则⊙O的半径的值是$\frac{4}{3}$.
如图,⊙O是Rt△ABC的内切圆,∠C=90°,BO的延长线交AC于点D,若BC=4,CD=2,则⊙O的半径的值是$\frac{4}{3}$.