题目内容
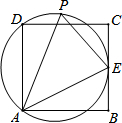 如图,已知在边长为8的正方形ABCD中,E是BC边的中点,P在过A、E、D三点的圆上,则△APE面积的最大值是( )
如图,已知在边长为8的正方形ABCD中,E是BC边的中点,P在过A、E、D三点的圆上,则△APE面积的最大值是( )A、10
| ||
B、10
| ||
| C、32 | ||
D、5
|
考点:正方形的性质,勾股定理,垂径定理
专题:
分析:设圆心为O,根据垂径定理点P在AE的垂直平分线上时,△APE面积的最大,过点E作EF⊥AD于F,连接AO,设圆的半径为r,在Rt△AOF中,利用勾股定理列式求出r,设PO与AE交点为G,利用勾股定理列式求出AE,再求出OG,然后求出PG的长度,再根据三角形的面积列式计算即可得解.
解答: 解:如图,设圆心为O,
解:如图,设圆心为O,
由垂径定理得,点P在AE的垂直平分线上时,点P到AE的距离最大,△APE面积的最大,
过点E作EF⊥AD于F,连接AO,
设圆的半径为r,
∵点E是BC的中点,
∴BE=
BC=
×8=4,
在Rt△AOF中,AO2=AF2+OF2,
即r2=42+(8-r)2,
解得r=5,
在Rt△ABE中,AE=
=
=4
,
设PO与AE交点为G,则AG=
AE=
×4
=2
,
在Rt△AOG中,OG=
=
=
,
∴PG=5+
,
∴△APE的最大面积=
×4
×(5+
)=10
+10.
故选A.
 解:如图,设圆心为O,
解:如图,设圆心为O,由垂径定理得,点P在AE的垂直平分线上时,点P到AE的距离最大,△APE面积的最大,
过点E作EF⊥AD于F,连接AO,
设圆的半径为r,
∵点E是BC的中点,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOF中,AO2=AF2+OF2,
即r2=42+(8-r)2,
解得r=5,
在Rt△ABE中,AE=
| AB2+BE2 |
| 82+42 |
| 5 |
设PO与AE交点为G,则AG=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
在Rt△AOG中,OG=
| AO2-AG2 |
52-(2
|
| 5 |
∴PG=5+
| 5 |
∴△APE的最大面积=
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
故选A.
点评:本题考查了正方形的性质,勾股定理,垂径定理,熟记各性质与定理并判断出三角形的面积最大时点P的位置是解题的关键,作出图形更形象直观.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
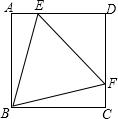 如图,正方形ABCD中,AB=4,点E,F分别在AD,DC上,且△BEF为等边三角形,则△EDF与△BFC的面积比为( )
如图,正方形ABCD中,AB=4,点E,F分别在AD,DC上,且△BEF为等边三角形,则△EDF与△BFC的面积比为( )| A、2:1 | B、3:1 |
| C、3:2 | D、5:3 |
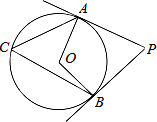 如图,AP、BP分别切⊙O于点A、B,∠P=60°,点C是圆上一动点,则∠C的度数为( )
如图,AP、BP分别切⊙O于点A、B,∠P=60°,点C是圆上一动点,则∠C的度数为( )| A、60 | B、40 |
| C、72° | D、60°或120° |
 如图,△ABC是等边三角形,D为BC上的一点,∠BAD=25°,△ABD经过旋转到达△ACE的位置,那么旋转角度为( )
如图,△ABC是等边三角形,D为BC上的一点,∠BAD=25°,△ABD经过旋转到达△ACE的位置,那么旋转角度为( )| A、25° | B、45° |
| C、60° | D、30° |
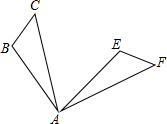 如图,△ABC绕点A顺时针旋转得到△AEF,若∠B=100°,∠F=50°,∠BAF=120°,则旋转的度数是( )
如图,△ABC绕点A顺时针旋转得到△AEF,若∠B=100°,∠F=50°,∠BAF=120°,则旋转的度数是( )| A、50 | B、60° |
| C、70° | D、90° |
要使分式
有意义,x的值是( )
| 1 |
| |x|-1 |
| A、x≠1 |
| B、x≠-1 |
| C、-1<x<1 |
| D、x≠1且x≠-1 |
 如图,P1、P2、P3…PK分别是抛物线y=x2上的点,其横坐标分别是1,2,3…K,记△OP1P2的面积为S1,△OP2P3的面积为S2,△OP3P4的面积为S3,则S10=
如图,P1、P2、P3…PK分别是抛物线y=x2上的点,其横坐标分别是1,2,3…K,记△OP1P2的面积为S1,△OP2P3的面积为S2,△OP3P4的面积为S3,则S10=