题目内容
 如图,P1、P2、P3…PK分别是抛物线y=x2上的点,其横坐标分别是1,2,3…K,记△OP1P2的面积为S1,△OP2P3的面积为S2,△OP3P4的面积为S3,则S10=
如图,P1、P2、P3…PK分别是抛物线y=x2上的点,其横坐标分别是1,2,3…K,记△OP1P2的面积为S1,△OP2P3的面积为S2,△OP3P4的面积为S3,则S10=考点:二次函数图象上点的坐标特征
专题:规律型
分析:求出点P11和点P10的坐标,然后根据S10等于以OP11和OP10为斜边的两个直角三角形的面积的差减去以P10P11为腰的直角梯形的面积,列式计算即可得解.
解答:解:由题意得,点P11(11,121),点P10(10,100),
S10=
×11×121-
×10×100-
×(100+121)×(11-10)
=
=
=55.
故答案为:55.
S10=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1331-1000-221 |
| 2 |
=
| 110 |
| 2 |
=55.
故答案为:55.
点评:本题考查了二次函数图象上点的坐标特征,仔细观察图形,得到相应三角形的面积的表示方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
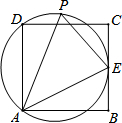 如图,已知在边长为8的正方形ABCD中,E是BC边的中点,P在过A、E、D三点的圆上,则△APE面积的最大值是( )
如图,已知在边长为8的正方形ABCD中,E是BC边的中点,P在过A、E、D三点的圆上,则△APE面积的最大值是( )A、10
| ||
B、10
| ||
| C、32 | ||
D、5
|
 如图,一圆与平面直角坐标系中的x轴切于点A,与y轴交于点B(0,4),C(0,16),该圆的半径为10,则A点的坐标为
如图,一圆与平面直角坐标系中的x轴切于点A,与y轴交于点B(0,4),C(0,16),该圆的半径为10,则A点的坐标为 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕DE,则AE的长为
如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕DE,则AE的长为