题目内容
6．$\sqrt{4}$-（π-3）0-（-1）2017+（-$\frac{1}{3}$）-2+tan60°+|$\sqrt{3}$-2|分析 原式利用平方根定义，零指数幂、负整数指数幂法则，绝对值的代数意义，以及乘方的意义计算即可得到结果．
解答 解：原式=2-1+1+9+$\sqrt{3}$+2-$\sqrt{3}$=13．
点评 此题考查了实数的运算，零指数幂、负整数指数幂，以及特殊角的三角函数值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
如图AB∥CD，BC∥DE，∠B=120°，则∠D的度数是60°．
1．-$\frac{1}{4}$的相反数是（ ）
| A． | 4 | B． | -$\frac{1}{4}$ | C． | $\frac{1}{4}$ | D． | -4 |
18．在实数0，（-$\sqrt{3}$）0，（-$\frac{2}{3}$）-2，|-2|中，最大的是（ ）
| A． | 0 | B． | （-$\sqrt{3}$）0 | C． | （-$\frac{2}{3}$）-2 | D． | |-2| |
15．
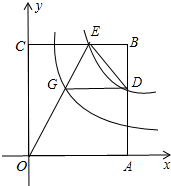矩形OABC有两边在坐标轴的正半轴上，如图所示，双曲线y=$\frac{6}{x}$与边AB、BC分别交于D、E两点，OE交双曲线y=$\frac{2}{x}$于点G，若DG∥OA，OA=3，则CE的长为（ ）
矩形OABC有两边在坐标轴的正半轴上，如图所示，双曲线y=$\frac{6}{x}$与边AB、BC分别交于D、E两点，OE交双曲线y=$\frac{2}{x}$于点G，若DG∥OA，OA=3，则CE的长为（ ）| A． | $\sqrt{2}$ | B． | 1.5 | C． | $\sqrt{3}$ | D． | 2 |