题目内容
4. 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动,过点A作AB⊥x轴于点B,以AB为斜边作Rt△ABC,则AB边上的中线CD的最小值为1.
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动,过点A作AB⊥x轴于点B,以AB为斜边作Rt△ABC,则AB边上的中线CD的最小值为1.
分析 先根据直角三角形斜边上的中线性质得到CD=$\frac{1}{2}$AB,再把抛物线解析式配成顶点式得到抛物线的顶点坐标为(1,2),从而得到垂线段AB的最小值为2,所以中线CD的最小值为1.
解答 解:∵CD为Rt△ABC中斜边AB边上的中线CD,
∴CD=$\frac{1}{2}$AB,
∵y=x2-2x+3=(x-1)2+2,
∴抛物线的顶点坐标为(1,2),
∴点A到x轴的最小距离为2,即垂线段AB的最小值为2,
∴中线CD的最小值为1.
故答案为1.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了直角三角形斜边上的中线性质.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
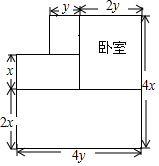 如图,是张老师买的经济适用房平面结构示意图,图中标明了有关尺寸(墙体厚度忽略不计,单位:m),房主计划把卧室以外的地面都铺上地砖,
如图,是张老师买的经济适用房平面结构示意图,图中标明了有关尺寸(墙体厚度忽略不计,单位:m),房主计划把卧室以外的地面都铺上地砖,
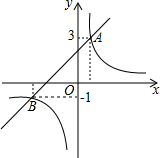 如图,直线l:y=x+2与双曲线C:y=$\frac{k}{x}$相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为-1.
如图,直线l:y=x+2与双曲线C:y=$\frac{k}{x}$相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为-1.