题目内容
19.计算或求值:(1)(x-3)3=27
(2)$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$.
分析 (1)通过立方运算,先求出(x-3)值,再求出x;
(2)先乘除,再把多项式中的二次根式化成最简二次根式,合并其中的同类二次根式.
解答 解:(1)法一:因为33=27,
所以x-3=3,
所以x=6
法二:x-3=$\root{3}{27}$
x-3=3
所以x=6.
(2)原式=$\sqrt{48÷3}$-$\sqrt{\frac{1}{2}×12}$+2$\sqrt{6}$
=$\sqrt{16}$-$\sqrt{6}$+2$\sqrt{6}$
=$4+\sqrt{6}$
点评 本题考查了立方根的定义、二次根式的加减乘除运算.二次根式的运算顺序:先乘除再加减,有括号先算括号里面的也可通过去括号法则去掉括号再计算.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
11.观察下列图形,照此规律,第5个图形中白色三角形的个数是( )


| A. | 81 | B. | 121 | C. | 161 | D. | 201 |
9. 如图,小聪坐在秋千上,秋千旋转了80°,小聪的位置也从P点运动到了P'点,则∠P'OP的度数为( )
如图,小聪坐在秋千上,秋千旋转了80°,小聪的位置也从P点运动到了P'点,则∠P'OP的度数为( )
 如图,小聪坐在秋千上,秋千旋转了80°,小聪的位置也从P点运动到了P'点,则∠P'OP的度数为( )
如图,小聪坐在秋千上,秋千旋转了80°,小聪的位置也从P点运动到了P'点,则∠P'OP的度数为( )| A. | 40° | B. | 50° | C. | 70° | D. | 80° |
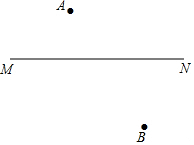 A、B为直线MN外两点,且在MN异侧,A、B到MN的距离不相等,试求一点P,满足下条件:
A、B为直线MN外两点,且在MN异侧,A、B到MN的距离不相等,试求一点P,满足下条件: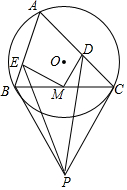 ⊙O是△ABG的外接圆,M是BC中点,PB,PC是⊙O切线,DM⊥ME.
⊙O是△ABG的外接圆,M是BC中点,PB,PC是⊙O切线,DM⊥ME. 如图,过x轴上一点A作平行于y轴的直线分别与抛物线y=$\frac{1}{4}$x2及y=x2交于B、C两点,若正方形BCDE的一边DE与y轴重合,则此正方形BCDE的面积为$\frac{16}{9}$.
如图,过x轴上一点A作平行于y轴的直线分别与抛物线y=$\frac{1}{4}$x2及y=x2交于B、C两点,若正方形BCDE的一边DE与y轴重合,则此正方形BCDE的面积为$\frac{16}{9}$. 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动,过点A作AB⊥x轴于点B,以AB为斜边作Rt△ABC,则AB边上的中线CD的最小值为1.
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动,过点A作AB⊥x轴于点B,以AB为斜边作Rt△ABC,则AB边上的中线CD的最小值为1. 已知:如图,AB=DC,AD=CB,在DA、BC的延长线上各任取一点E,F,连接EF.
已知:如图,AB=DC,AD=CB,在DA、BC的延长线上各任取一点E,F,连接EF.