题目内容
19．下面每一组数据中的三个数值分别为三角形的三边长，不能构成直角三角形的是（ ）| A． | $\sqrt{3}$，2，$\sqrt{5}$ | B． | 6，8，10 | C． | 3，4，5 | D． | 5，12，13 |
分析 求证是否为直角三角形，这里给出三边的长，只要验证两小边的平方和等于最长边的平方即可．
解答 解：A、22+（$\sqrt{3}$）2≠（$\sqrt{5}$）2，不能构成直角三角形，故此选项正确；
B、62+82=102，能构成直角三角形，故此选项错误；
C、32+42=52，能构成直角三角形，故此选项错误；
D、52+122=132，能构成直角三角形，故此选项错误；
故选A．
点评 本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．
练习册系列答案
相关题目
9．对于二次函数y=x2-2mx-3，下列结论错误的是（ ）
| A． | 它的图象与x轴有两个交点 | B． | 方程x2-2mx=3的两根之积为-3 | ||
| C． | 它的图象的对称轴在y轴的右侧 | D． | x＜m时，y随x的增大而减小 |
14．
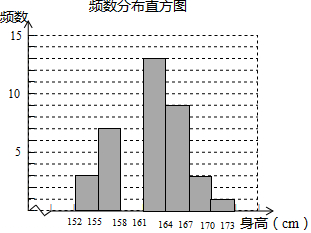某体育老师测量了自己任教的甲、乙两班男生的身高，并制作了如下不完整的统计图表．
根据以上统计图表完成下列问题：
（1）统计表中m=14，n=0.26，并将频数分布直方图补充完整；
（2）在这次测量中两班男生身高的中位数在：161≤x＜164范围内；
（3）在身高≥167cm的4人中，甲、乙两班各有2人，现从4人中随机推选2人补充到学校国旗护卫队中，请用列表或画树状图的方法求出这两人都来自相同班级的概率．
某体育老师测量了自己任教的甲、乙两班男生的身高，并制作了如下不完整的统计图表．| 身高分组 | 频数 | 频率 |
| 152≤x＜155 | 3 | 0.06 |
| 155≤x＜158 | 7 | 0.14 |
| 158≤x＜161 | m | 0.28 |
| 161≤x＜164 | 13 | n |
| 164≤x＜167 | 9 | 0.18 |
| 167≤x＜170 | 3 | 0.06 |
| 170≤x＜173 | 1 | 0.02 |
（1）统计表中m=14，n=0.26，并将频数分布直方图补充完整；
（2）在这次测量中两班男生身高的中位数在：161≤x＜164范围内；
（3）在身高≥167cm的4人中，甲、乙两班各有2人，现从4人中随机推选2人补充到学校国旗护卫队中，请用列表或画树状图的方法求出这两人都来自相同班级的概率．
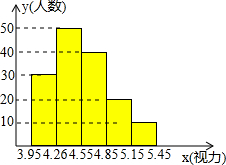当今，青少年视力水平下降已引起了社会的关注，为了了解某校3000名学生的视力情况，从中抽取了一部分学生进行一次抽样调查，利用所得数据绘制的直方图（长方形的高表示该组人数）如图所示：
