题目内容
4.已知抛物线C1:y=x2-3x-10及抛物线C2:y=x2-(2a+2)x+a2+2a(其中a为常数).当-2<x<a+2时,C1、C2的图象都在x轴下方,则a的取值范围是-4<a≤-2.分析 根据已知条件得到抛物线C1与x轴的交点坐标为(-2,0),(5,0),解方程x2-(2a+2)x+a2+2a=0,得到x1=a,x2=a+2,由于当-2<x<a+2时,C1、C2的图象都在x轴下方,得到$\left\{\begin{array}{l}{a≤-2}\\{a+2>-2}\\{a+2≤5}\end{array}\right.$,于是得到结论.
解答 解:在y=x2-3x-10中,令y=0,则x2-3x-10=0,
解得:x1=-2,x2=5,
∴抛物线C1与x轴的交点坐标为(-2,0),(5,0),
在y=x2-(2a+2)x+a2+2a中,令y=0,则x2-(2a+2)x+a2+2a=0,
解得:x1=a,x2=a+2,
∵当-2<x<a+2时,C1、C2的图象都在x轴下方,
∴$\left\{\begin{array}{l}{a≤-2}\\{a+2>-2}\\{a+2≤5}\end{array}\right.$,
解得:-4<a≤-2,
∴a的取值范围是:-4<a≤-2.
点评 本题考查了抛物线与x轴的交点问题,不等式组的解法,二次函数的性质,正确的理解题意是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下面每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )
| A. | $\sqrt{3}$,2,$\sqrt{5}$ | B. | 6,8,10 | C. | 3,4,5 | D. | 5,12,13 |
12.下列图形中不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程ax2+bx+c+2=0无实数根;③a-b+c≥0; ④$\frac{a+b+c}{b-a}$的最小值为3.其中正确的是( )
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②③④ |
14.下表是全国7个城市2017年3月份某日空气质量指数(AQI)的统计结果:
该日空气质量指数的中位数是( )
| 城市 | 北京 | 成都 | 深圳 | 长沙 | 上海 | 武汉 | 广州 |
| AQI指数 | 25 | 72 | 49 | 241 | 62 | 185 | 49 |
| A. | 49 | B. | 62 | C. | 241 | D. | 97 |
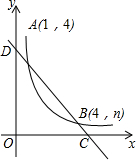 如图,直线y1=ax+b与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于A(1,4)、B(4,n)两点,与x轴、y轴交于C、D两点.
如图,直线y1=ax+b与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于A(1,4)、B(4,n)两点,与x轴、y轴交于C、D两点.