Question

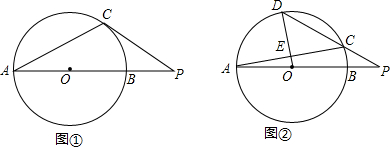
9．在⊙O中，AB为直径，C为⊙O上一点．
（1）如图①，过点C作⊙O的切线，与AB的延长线相交于点P，若∠CAB=28°，求∠P的大小；
（2）如图②，D为$\widehat{AC}$上一点，且OD经过AC的中点E，连接DC并延长，与AB的延长线相交于点P，若∠CAB=10°，求∠P的大小．

Answer 1

分析 （1）首先连接OC，由OA=OC，即可求得∠A的度数，然后由圆周角定理，求得∠POC的度数，继而求得答案；
（2）由AE=CE，OD为半径，可得OD⊥AC，继而求得答案．

解答 解：（1）连接OC，
∵OA=OC，
∴∠A=∠OCA=28°，
∴∠POC=56°，
∵CP是⊙O的切线，
∴∠OCP=90°，
∴∠P=34°；

（2）∵AE=CE，OD为半径，
∴OD⊥AC，
∵∠CAB=10°，
∴∠AOE=80°，
∴∠DCA=40°，
∵∠P=∠DCA-∠CAB，
∴∠P=30°．

点评 此题考查了切线的性质以及等腰三角形的性质．注意准确作出辅助线是解此题的关键．