题目内容
2.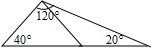 如图过三角形一个顶点画一条直线,把这个三角形分别分成两个等腰三角形.
如图过三角形一个顶点画一条直线,把这个三角形分别分成两个等腰三角形.
分析 如图2,①以点C为顶点,作∠ACD=∠A=40°,则直线CD即为所求;
②如图3,以点C为顶点,作∠BCD=∠B=20°,则直线CD即为所求.
解答 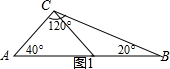 解:如图1,已知∠A=40°,∠B=20°,∠ACB=120,
解:如图1,已知∠A=40°,∠B=20°,∠ACB=120,
求作:直线CD,使△ACD和△BCD是等腰三角形.
作法:如图2,①以点C为顶点,作∠ACD=∠A=40°,则直线CD即为所求;
证明:∵∠ACD=∠A=40°,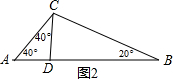
∴∠DCB=120°-∠ACD=80°,
∵∠BDC=∠A+∠ACD=80°,
∴∠BDC=∠BCD,
∴△ACD与△BCD为等腰三角形;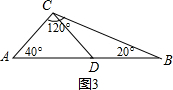
②如图3,以点C为顶点,作∠BCD=∠B=20°,则直线CD即为所求;
证明:∵∠BCD=20°,
∴∠CDA=40°,
∴∠A=∠CDA,
∴△ACD与△BCD是等腰三角形.
点评 本题考查了等腰三角形的判定,作图-复杂作图,熟练掌握等腰三角形的判定定理是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
12.若关于x的方程$\frac{ax}{x-2}$=$\frac{4}{x-2}$+1无解,则a的值是( )
| A. | 5 | B. | -5 | C. | -4 | D. | 2 |
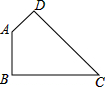 如图,在四边形ABCD中,∠BAD=135°,∠ABC=∠ADC=90°,DC=6,AD=2,求四边形ABCD的面积.
如图,在四边形ABCD中,∠BAD=135°,∠ABC=∠ADC=90°,DC=6,AD=2,求四边形ABCD的面积.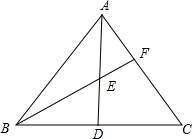 如图,AD是△ABC的中线,E为AD的中点,连接BE并延长,交AC于F,AF=$\frac{1}{3}$AC.求证:EF=$\frac{1}{4}$BF.
如图,AD是△ABC的中线,E为AD的中点,连接BE并延长,交AC于F,AF=$\frac{1}{3}$AC.求证:EF=$\frac{1}{4}$BF.