题目内容
如图,在Rt△ABC中,BC=(2+
)cm,∠B=15°,求AC的长.
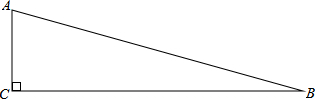
| 3 |

考点:勾股定理,含30度角的直角三角形
专题:
分析:作线段AB的垂直平分线DE,连接AD,根据线段垂直平分线的性质可知AD=BD,故∠B=∠BAD=15°,由三角形外角的性质可知∠ADC=30°,所以AD=2AC,CD=BC-BD=BC-2AC,再根据勾股定理即可得出结论.
解答:
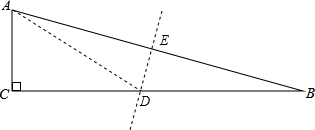 解:作线段AB的垂直平分线DE,连接AD,则AD=BD,故∠B=∠BAD=15°,
解:作线段AB的垂直平分线DE,连接AD,则AD=BD,故∠B=∠BAD=15°,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=30°,
∴AD=2AC,CD=
AC,
∵AD+CD=BC,即2AC+
AC=2+
,解得AC=1.
 解:作线段AB的垂直平分线DE,连接AD,则AD=BD,故∠B=∠BAD=15°,
解:作线段AB的垂直平分线DE,连接AD,则AD=BD,故∠B=∠BAD=15°,∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=30°,
∴AD=2AC,CD=
| 3 |
∵AD+CD=BC,即2AC+
| 3 |
| 3 |
点评:本题考查的是勾股定理,根据题意构造出特殊角是解答此题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
如图,在数轴上有六个点,且AB=BC=CD=DE=EF,则与点C所表示的数最接近的整数是( )

| A、2 | B、1 | C、0 | D、-1 |
 如图,在四边形ABCD中,∠1=∠2,∠3=∠4,∠B=∠D,AF=CE,AB∥CD.
如图,在四边形ABCD中,∠1=∠2,∠3=∠4,∠B=∠D,AF=CE,AB∥CD.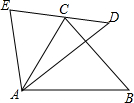 如图,E、C、D三点在一条直线上,AE=AC,AD=AB,∠EAC=∠DAB.求证:△EAD≌△CAB.
如图,E、C、D三点在一条直线上,AE=AC,AD=AB,∠EAC=∠DAB.求证:△EAD≌△CAB.
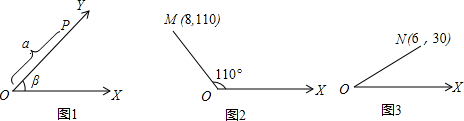
 如图,AB是⊙O的直径,CD是弦,且AB⊥CD,若∠BOC=50°,则∠A=
如图,AB是⊙O的直径,CD是弦,且AB⊥CD,若∠BOC=50°,则∠A= 如图,直线y=x+4与抛物线y=-x2+10相交于A(2,6),B(-3,1)两点,与y轴相交于点C,过点C作直线l交抛物线于E、F两点,是否存在直线l,使S△EOC:S△FOC=1:3?若存在,求直线l的解析式;若不存在,请说明理由.
如图,直线y=x+4与抛物线y=-x2+10相交于A(2,6),B(-3,1)两点,与y轴相交于点C,过点C作直线l交抛物线于E、F两点,是否存在直线l,使S△EOC:S△FOC=1:3?若存在,求直线l的解析式;若不存在,请说明理由.