Question

20．小红将笔记本电脑水平放置在桌子上，显示屏OB与底板OA所在的水平线的夹角为120°时，感觉最舒适（如图1），侧面示意图为图2；使用时为了散热，她在底板下垫入散热架sin43°≈0.6820后，电脑转到cos43°≈0.7314位置（如图3），侧面示意图为图4．已知OA=OB=24cm，tan43°≈0.9325于点C，O′C=12cm．

（1）求∠CAO′的度数；
（2）显示屏的顶部B′比原来升高了多少？
（3）如图4，垫入散热架后，要使显示屏O′B′与水平线的夹角仍保持120°，则显示屏O′B′应绕点O′按顺时针方向旋转多少度？

Answer 1

分析 （1）通过解直角三角形即可得到结果；
（2）过点B作BD⊥AO交AO的延长线于D，通过解直角三角形求得BD，由C、O′、B′三点共线可得结果；
（3）显示屏O′B′应绕点O′按顺时针方向旋转30°，求得∠EO′B′=∠FO′A=30°，既是显示屏O′B′应绕点O′按顺时针方向旋转30°．

解答 解：（1）∵O′C⊥OA于C，OA=OB=24cm，O’C=12，
∴$sin∠CAO'=\frac{O'C}{O'A}=\frac{O'C}{OA}=\frac{12}{24}=\frac{1}{2}$．
∴∠CAO'=30°．
（2）如图，过点B作BD⊥AO交AO的延长线于点D．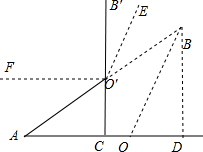

∵$sin∠BOD=\frac{BD}{OB}$，
∴BD=OB•sin∠BOD．
∵∠AOB=120°，
∴∠BOD=60°．
∴$BD=OB•sin∠BOD=24×\frac{{\sqrt{3}}}{2}=12\sqrt{3}$．
∴显示屏的顶部B'比原来升高了$（{36-12\sqrt{3}}）$cm．
（3）显示屏O'B'应绕点O'按顺时针方向旋转30°．
理由如下：
如图，电脑显示屏O'B’绕点O'按顺时针方向旋转α度至O'E处，O'F∥OA．

∵电脑显示屏O'B’与水平线的夹角仍保持120°，
∴∠EO'F=120°．
∴∠FO'A=∠CAO'=30°．
∴∠AO'B'=120°．
∴∠EO'B'=∠FO'A=30°，即α=30°．
∴显示屏O'B'应绕点O'按顺时针方向旋转30°．

点评 本题考查了解直角三角形的应用，旋转的性质，正确的画出图形是解题的关键．