题目内容
12. 如图,在△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,AD∥BC,且DE=CF,求证:BE=AF.
如图,在△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,AD∥BC,且DE=CF,求证:BE=AF.
分析 欲证:BE=AF,则证明两个角所在的两三角形全等即可.
解答 证明:∵AD∥BC,
∴∠D=∠C,
∵DE=CF,
∴DE+EF=CF+EF,
∴DF=CE,
在△DAF和△CBE中,
$\left\{\begin{array}{l}{∠A=∠B}\\{∠D=∠C}\\{DF=EC}\end{array}\right.$,
∴△DAF≌△CBE,
∴BE=AF.
点评 本题主要考查三角形全等的判定和全等三角形的对应边相等;要牢固掌握并灵活运用这些知识.

练习册系列答案
相关题目
1.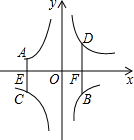 如图,A,B两点在反比例函数y=$\frac{{k}_{1}}{x}$的图象上,C、D两点在反比例函数y=$\frac{{k}_{2}}{x}$的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=$\frac{10}{3}$,则k2-k1=( )
如图,A,B两点在反比例函数y=$\frac{{k}_{1}}{x}$的图象上,C、D两点在反比例函数y=$\frac{{k}_{2}}{x}$的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=$\frac{10}{3}$,则k2-k1=( )
 如图,A,B两点在反比例函数y=$\frac{{k}_{1}}{x}$的图象上,C、D两点在反比例函数y=$\frac{{k}_{2}}{x}$的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=$\frac{10}{3}$,则k2-k1=( )
如图,A,B两点在反比例函数y=$\frac{{k}_{1}}{x}$的图象上,C、D两点在反比例函数y=$\frac{{k}_{2}}{x}$的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=$\frac{10}{3}$,则k2-k1=( )| A. | 4 | B. | $\frac{14}{3}$ | C. | $\frac{16}{3}$ | D. | 6 |

 如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.
如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.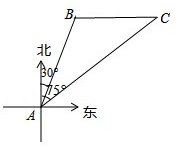 南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?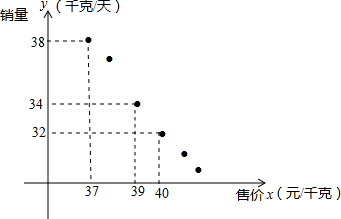 某进口专营店销售一种“特产”,其成本价是20元/千克,根据以往的销售情况描出销量y(千克/天)与售价x(元/千克)的关系,如图所示.
某进口专营店销售一种“特产”,其成本价是20元/千克,根据以往的销售情况描出销量y(千克/天)与售价x(元/千克)的关系,如图所示.