题目内容
8．
如图，一直线与两坐标轴的正半轴分别交于A，B两点，P是线段AB上任意一点（不包括端点），过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10，则该直线的函数表达式是（ ）| A． | y=x+5 | B． | y=x+10 | C． | y=-x+5 | D． | y=-x+10 |
分析 设P点坐标为（x，y），由坐标的意义可知PC=x，PD=y，根据题意可得到x、y之间的关系式，可得出答案．
解答 
解：
设P点坐标为（x，y），如图，过P点分别作PD⊥x轴，PC⊥y轴，垂足分别为D、C，
∵P点在第一象限，
∴PD=y，PC=x，
∵矩形PDOC的周长为10，
∴2（x+y）=10，
∴x+y=5，即y=-x+5，
故选C．
点评 本题主要考查矩形的性质及点的坐标的意义，根据坐标的意义得出x、y之间的关系是解题的关键．
练习册系列答案
相关题目
18．
如图，l1∥l2，将直角三角板如图所示的方式放置，则∠1+∠2=（ ）
如图，l1∥l2，将直角三角板如图所示的方式放置，则∠1+∠2=（ ）| A． | 75° | B． | 80° | C． | 90° | D． | 100° |
19．已知反比例函数y=$\frac{k}{x}$的图象经过点（-1，3），那么这个函数图象一定还经过点（ ）
| A． | （3，1） | B． | （1，-3） | C． | （-1，-3） | D． | （-3，-1） |
如图，已知抛物线y=ax2+bx+c（a≠0）经过A（-3，0）、B（5，0）、C（0，5）三点，O为坐标原点
如图1，一枚质地均匀的正四面体骰子，它有四个面并分别标有数字1，2，3，4．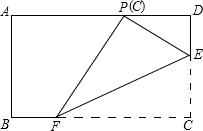
如图，在矩形ABCD中，点E、F分别在边CD、BC上，且DC=3DE=3a．将矩形沿直线EF折叠，使点C恰好落在AD边上的点P处，则FP=2$\sqrt{3}$a．