题目内容
10. 如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为3m.
如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为3m.
分析 根据CD∥AB∥MN,得到△ABE∽△CDE,△ABF∽△MNF,根据相似三角形的性质可知$\frac{CD}{AB}=\frac{DE}{BE}$,$\frac{FN}{FB}=\frac{MN}{AB}$,即可得到结论.
解答  解:如图,∵CD∥AB∥MN,
解:如图,∵CD∥AB∥MN,
∴△ABE∽△CDE,△ABF∽△MNF,
∴$\frac{CD}{AB}=\frac{DE}{BE}$,$\frac{FN}{FB}=\frac{MN}{AB}$,
即$\frac{1.8}{AB}=\frac{1.8}{1.8+BD}$,$\frac{1.5}{AB}=\frac{1.5}{1.5+2.7-BD}$,
解得:AB=3m.
答:路灯的高为3m.
点评 本题考查了中心投影,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.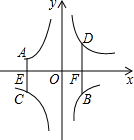 如图,A,B两点在反比例函数y=$\frac{{k}_{1}}{x}$的图象上,C、D两点在反比例函数y=$\frac{{k}_{2}}{x}$的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=$\frac{10}{3}$,则k2-k1=( )
如图,A,B两点在反比例函数y=$\frac{{k}_{1}}{x}$的图象上,C、D两点在反比例函数y=$\frac{{k}_{2}}{x}$的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=$\frac{10}{3}$,则k2-k1=( )
 如图,A,B两点在反比例函数y=$\frac{{k}_{1}}{x}$的图象上,C、D两点在反比例函数y=$\frac{{k}_{2}}{x}$的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=$\frac{10}{3}$,则k2-k1=( )
如图,A,B两点在反比例函数y=$\frac{{k}_{1}}{x}$的图象上,C、D两点在反比例函数y=$\frac{{k}_{2}}{x}$的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=$\frac{10}{3}$,则k2-k1=( )| A. | 4 | B. | $\frac{14}{3}$ | C. | $\frac{16}{3}$ | D. | 6 |
5. 实数a,b在数轴上的对应点的位置如图所示,则正确的结论是( )
实数a,b在数轴上的对应点的位置如图所示,则正确的结论是( )
 实数a,b在数轴上的对应点的位置如图所示,则正确的结论是( )
实数a,b在数轴上的对应点的位置如图所示,则正确的结论是( )| A. | a>-2 | B. | a<-3 | C. | a>-b | D. | a<-b |
15.不等式组$\left\{\begin{array}{l}{x-1>0}\\{x≤2}\end{array}\right.$的解集是( )
| A. | x≤2 | B. | x>1 | C. | 1<x≤2 | D. | 无解 |

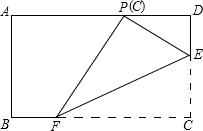 如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=3a.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP=2$\sqrt{3}$a.
如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=3a.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP=2$\sqrt{3}$a.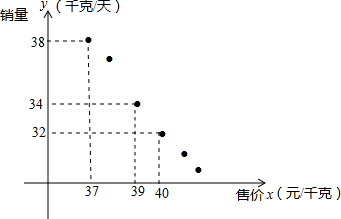 某进口专营店销售一种“特产”,其成本价是20元/千克,根据以往的销售情况描出销量y(千克/天)与售价x(元/千克)的关系,如图所示.
某进口专营店销售一种“特产”,其成本价是20元/千克,根据以往的销售情况描出销量y(千克/天)与售价x(元/千克)的关系,如图所示. 如图,已知直线a∥b,△ABC的顶点B在直线b上,∠C=90°,∠1=36°,则∠2的度数是54°.
如图,已知直线a∥b,△ABC的顶点B在直线b上,∠C=90°,∠1=36°,则∠2的度数是54°.