题目内容
8. 如图,D、E、F分别是△ABC的AB、AC、BC上的中点,若AB=7,BC=6,AC=5,则△DEF的周长是9.
如图,D、E、F分别是△ABC的AB、AC、BC上的中点,若AB=7,BC=6,AC=5,则△DEF的周长是9.
分析 根据D、E、F分别是AB、AC、BC的中点,可以判断DF、FE、DE为三角形中位线,利用中位线定理求出DF、FE、DE与AC、AB、CB的长度关系即可解答.
解答 解:∵D、E、F分别是AB、AC、BC的中点,
∴ED、FE、DF为△ABC中位线,
∴DF=$\frac{1}{2}$AC,FE=$\frac{1}{2}$AB,DE=$\frac{1}{2}$BC;
∴DF+FE+DE=$\frac{1}{2}$AC+$\frac{1}{2}$AB+$\frac{1}{2}$BC=$\frac{1}{2}$(AC+BA+CB)=$\frac{1}{2}$×(6+7+5)=9.
故答案为:9.
点评 本题考查了三角形的中位线定理,根据中点判断出中位线,再利用中位线定理是解题的基本思路.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
13.掷一枚质地均匀的硬币10次,下列说法正确的是( )
| A. | 有5次正面朝上 | B. | 不可能10次正面朝上 | ||
| C. | 不可能10次正面朝下 | D. | 可能有5次正面朝上 |
18.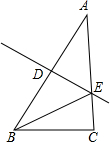 如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,且AC=10,BC=4,则△BCE的周长为( )
如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,且AC=10,BC=4,则△BCE的周长为( )
 如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,且AC=10,BC=4,则△BCE的周长为( )
如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,且AC=10,BC=4,则△BCE的周长为( )| A. | 6 | B. | 14 | C. | 18 | D. | 24 |
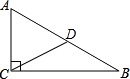 如图所示,在△ABC中,∠ACB=90°,BC=5cm,AC=10cm,CD为中线,以点C为圆心,以$\frac{5}{2}$$\sqrt{5}$cm为半径作圆,则点A,B,D与⊙C的位置关系如何.
如图所示,在△ABC中,∠ACB=90°,BC=5cm,AC=10cm,CD为中线,以点C为圆心,以$\frac{5}{2}$$\sqrt{5}$cm为半径作圆,则点A,B,D与⊙C的位置关系如何.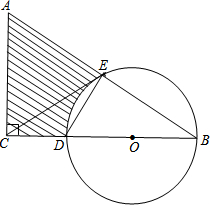 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=3,斜边AB的垂直平分线交BC与点D,交AB与点E,以BD为直径作⊙O,连接CE.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=3,斜边AB的垂直平分线交BC与点D,交AB与点E,以BD为直径作⊙O,连接CE.
 如图,在直角坐标系xOy中,直线y=mx与双曲线y=$\frac{n}{x}$相交于A(-2,a),B两点,BC⊥x轴,垂足为C,△AOC的面积是3.
如图,在直角坐标系xOy中,直线y=mx与双曲线y=$\frac{n}{x}$相交于A(-2,a),B两点,BC⊥x轴,垂足为C,△AOC的面积是3.