题目内容
10.在平面直角坐标系中,将线段OA绕原点旋转90°,已知OA=2且与x轴正半轴的夹角是30°,记点A的对应点为A1,则A1的坐标为(1,-$\sqrt{3}$)或(-1,$\sqrt{3}$).分析 从线段OA绕原点顺时针旋转90°和线段OA绕原点逆时针旋转90°两种情况进行分析,结合直角三角形的性质解答即可.
解答 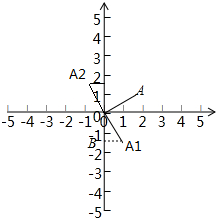 解:当线段OA绕原点顺时针旋转90°时,
解:当线段OA绕原点顺时针旋转90°时,
作A1B⊥y轴于点B,
由题意得,∠A1OB=30°,OA1=2,
∴A1B=1,OB=$\sqrt{3}$,
∴A1的坐标为:(1,-$\sqrt{3}$);
当线段OA绕原点逆时针旋转90°时,
同理可知,此时A1的坐标为:(-1,$\sqrt{3}$),
故答案为:(1,-$\sqrt{3}$)或(-1,$\sqrt{3}$).
点评 本题考查的是坐标与图形的变化即旋转的知识,掌握旋转的旋转是解题的关键,注意直角三角形的性质的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20. 从上面观察这个立体图形,能得到的平面图形是( )
从上面观察这个立体图形,能得到的平面图形是( )
 从上面观察这个立体图形,能得到的平面图形是( )
从上面观察这个立体图形,能得到的平面图形是( )| A. |  | B. |  | C. |  | D. |  |
1.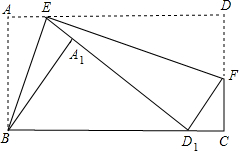 已知矩形ABCD中,AB=4,AD=7,点E是边AD上的点,点F是边DC上的点,分别沿BE,EF折叠得得到点A1,D1,恰好使D1落在BC上,且E,A1,D1同线,AE>2,则AE=( )
已知矩形ABCD中,AB=4,AD=7,点E是边AD上的点,点F是边DC上的点,分别沿BE,EF折叠得得到点A1,D1,恰好使D1落在BC上,且E,A1,D1同线,AE>2,则AE=( )
 已知矩形ABCD中,AB=4,AD=7,点E是边AD上的点,点F是边DC上的点,分别沿BE,EF折叠得得到点A1,D1,恰好使D1落在BC上,且E,A1,D1同线,AE>2,则AE=( )
已知矩形ABCD中,AB=4,AD=7,点E是边AD上的点,点F是边DC上的点,分别沿BE,EF折叠得得到点A1,D1,恰好使D1落在BC上,且E,A1,D1同线,AE>2,则AE=( )| A. | $\frac{7}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{9}{4}$ | D. | $\frac{5}{2}$ |
15. 如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( )
如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( )
 如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( )
如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( )| A. | CD+DF=4 | B. | CD-DF=2$\sqrt{3}$-3 | C. | BC+AB=2$\sqrt{3}$+4 | D. | BC-AB=2 |
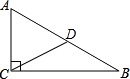 如图所示,在△ABC中,∠ACB=90°,BC=5cm,AC=10cm,CD为中线,以点C为圆心,以$\frac{5}{2}$$\sqrt{5}$cm为半径作圆,则点A,B,D与⊙C的位置关系如何.
如图所示,在△ABC中,∠ACB=90°,BC=5cm,AC=10cm,CD为中线,以点C为圆心,以$\frac{5}{2}$$\sqrt{5}$cm为半径作圆,则点A,B,D与⊙C的位置关系如何.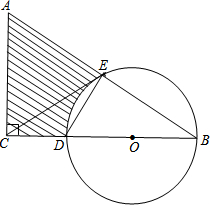 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=3,斜边AB的垂直平分线交BC与点D,交AB与点E,以BD为直径作⊙O,连接CE.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=3,斜边AB的垂直平分线交BC与点D,交AB与点E,以BD为直径作⊙O,连接CE. 如图,在直角坐标系xOy中,直线y=mx与双曲线y=$\frac{n}{x}$相交于A(-2,a),B两点,BC⊥x轴,垂足为C,△AOC的面积是3.
如图,在直角坐标系xOy中,直线y=mx与双曲线y=$\frac{n}{x}$相交于A(-2,a),B两点,BC⊥x轴,垂足为C,△AOC的面积是3.