题目内容
19.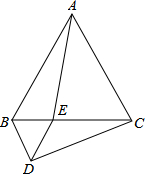 如图所示,△ABC和△BDE都是等边三角形,AE与CD相等吗?说明理由.
如图所示,△ABC和△BDE都是等边三角形,AE与CD相等吗?说明理由.
分析 根据等边三角形各边长相等的性质,可得AB=BC,BE=BD,根据等边三角形各内角为60°可得∠ABE=∠DBE,进而求证△ABE≌△CBD(SAS),即可求得AE=CD;
解答 证明:∵△ABC是等边三角形,
∴AB=BC,∠ABE=60°
又∵△BDE是等边三角形,
∴BE=BD,∠DBE=60°,
∴∠ABE=∠DBE,
在△ABE和△CBD中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠DBE}\\{BE=BD}\end{array}\right.$,
∴△ABE≌△CBD(SAS),
∴AE=CD.
点评 本题主要考查对全等三角形的性质和判定,等边三角形的面积等知识点的理解和掌握,熟练地运用性质进行推理是解此题的关键.

练习册系列答案
相关题目
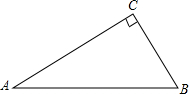 如图,△ABC中,∠ACB=90°,BC=$\sqrt{5}$,AC=2$\sqrt{5}$,
如图,△ABC中,∠ACB=90°,BC=$\sqrt{5}$,AC=2$\sqrt{5}$,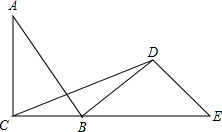 如图,点C,B,E在同一条直线上,AC⊥BC,BD⊥DE,AC=BD=6,AB=10,∠A=∠DBE
如图,点C,B,E在同一条直线上,AC⊥BC,BD⊥DE,AC=BD=6,AB=10,∠A=∠DBE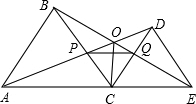 如图,C为线段AE上一动点(不与点A,E重合),在AE在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤OC平分∠AOE.一定成立的结论有①②③⑤.
如图,C为线段AE上一动点(不与点A,E重合),在AE在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤OC平分∠AOE.一定成立的结论有①②③⑤.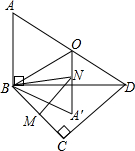 如图,一副三角板△BCD拼在一起,O为AD的中点,AB=4,将△ABO沿BO对折到△A′BO处,M为边BC上一动点,N为直线A′O一动点,则NB+NM的最小值为2$\sqrt{6}$.
如图,一副三角板△BCD拼在一起,O为AD的中点,AB=4,将△ABO沿BO对折到△A′BO处,M为边BC上一动点,N为直线A′O一动点,则NB+NM的最小值为2$\sqrt{6}$.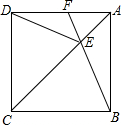 如图,正方形ABCD中,点E在对角线AC上,连接EB、ED.
如图,正方形ABCD中,点E在对角线AC上,连接EB、ED.