题目内容
14.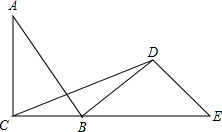 如图,点C,B,E在同一条直线上,AC⊥BC,BD⊥DE,AC=BD=6,AB=10,∠A=∠DBE
如图,点C,B,E在同一条直线上,AC⊥BC,BD⊥DE,AC=BD=6,AB=10,∠A=∠DBE(1)求证:AB∥DE;
(2)求CE的长;
(3)求△DBC的面积.
分析 (1)根据三角形全等得到内错角相等,证得AB∥DE;
(2)由全等三角形的性质得到对应边相等,求得BE长度,根据勾股定理求得BC的长度,可得结论;
(3)根据面积公式求得BC边上的高,再由面积公式求出结果.
解答 解;(1)证明:在△ACB与△BDE中,
$\left\{\begin{array}{l}{∠A=DBE}\\{AC=BD}\\{∠ACB=∠BDE}\end{array}\right.$,
∴△ACB≌△BDE,
∴∠ABC=∠E,
∴AB∥DE;
(2)∵AC=BD=6,AB=10,
由(1)知△ACB≌△BDE,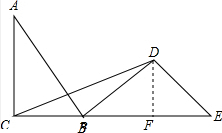
∴BE=AB=10,
∴BC=$\sqrt{{AB}^{2}{-AC}^{2}}$=8,
∴CE=18;
(3)如图过D作DF⊥CE于F,
∴DF=$\frac{6×8}{10}$$\frac{24}{5}$,
∴S△DBC=$\frac{1}{2}$×$\frac{24}{5}$×8=$\frac{96}{5}$.
点评 本题考查了平行线的判定,勾股定理的应用,全等三角形的判定与性质,三角形的面积公式的应用,关键是证明三角形全等.

练习册系列答案
相关题目
2. 如图:△ABC中,DE∥BC,AD=5,BD=10,AE=3.则AC的值为( )
如图:△ABC中,DE∥BC,AD=5,BD=10,AE=3.则AC的值为( )
 如图:△ABC中,DE∥BC,AD=5,BD=10,AE=3.则AC的值为( )
如图:△ABC中,DE∥BC,AD=5,BD=10,AE=3.则AC的值为( )| A. | 9 | B. | 6 | C. | 3 | D. | 4 |
3.2014年12月26日,南宁至广州高速铁路开始运行,从南宁到广州,乘空调快车的行程为872km,高铁开通后,高铁列车的行程约为580km,运行时间比空调快车时间少了8h.若高铁列车的平均速度是空调快车的2.5倍,求高铁列车的平均速度.设空调快车平均速度为xkm/h,则根据题意所列方程正确的是( )
| A. | $\frac{580}{2.5x}=\frac{872}{x}-8$ | B. | $\frac{580}{2.5x}=\frac{872}{x}+8$ | C. | $\frac{580}{x}=\frac{872}{2.5x}-8$ | D. | $\frac{580}{x}=\frac{872}{2.5x}+8$ |
4.计算$\sqrt{(-2)^{2}}$的结果是( )
| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
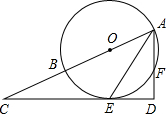 如图,AB为⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
如图,AB为⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.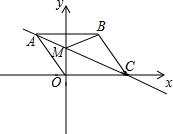 已知:如图平面直角坐标系xOy中,C在x轴上,四边形OABC为菱形,且A点坐标
已知:如图平面直角坐标系xOy中,C在x轴上,四边形OABC为菱形,且A点坐标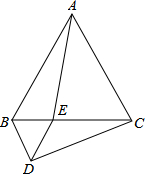 如图所示,△ABC和△BDE都是等边三角形,AE与CD相等吗?说明理由.
如图所示,△ABC和△BDE都是等边三角形,AE与CD相等吗?说明理由.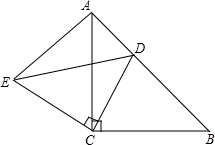 已知:如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点,求∠EAC的度数.
已知:如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点,求∠EAC的度数.