��Ŀ����
����˵����,��ȷ����(����)
A. ����ij��ֱ�߶ԳƵ�������������ȫ��������
B. ȫ�ȵ������������ǹ���ij��ֱ�߶ԳƵ�
C. ����ͼ�ι���ij��ֱ�߶Գ�,��������ͼ��һ���ֱ�λ������ֱ�ߵ�����
D. ȫ�ȵ�����ͼ��һ������Գ�
 A
��������A. ����ij��ֱ�߶ԳƵ�������������ȫ�������Σ���ȷ��
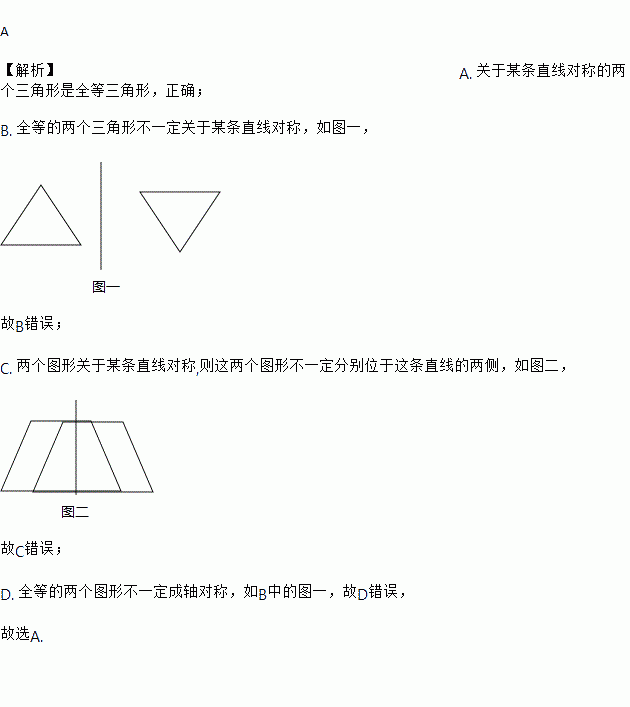
B. ȫ�ȵ����������β�һ������ij��ֱ�߶Գƣ���ͼһ��
��B����
C. ����ͼ�ι���ij��ֱ�߶Գ�,��������ͼ�β�һ���ֱ�λ������ֱ�ߵ����࣬��ͼ����
��C����
D. ȫ�ȵ�����ͼ�β�һ������Գƣ���B�е�ͼһ����D����
��ѡA.
A
��������A. ����ij��ֱ�߶ԳƵ�������������ȫ�������Σ���ȷ��
B. ȫ�ȵ����������β�һ������ij��ֱ�߶Գƣ���ͼһ��
��B����
C. ����ͼ�ι���ij��ֱ�߶Գ�,��������ͼ�β�һ���ֱ�λ������ֱ�ߵ����࣬��ͼ����
��C����
D. ȫ�ȵ�����ͼ�β�һ������Գƣ���B�е�ͼһ����D����
��ѡA.
 ��������������������ϵ�д�
��������������������ϵ�д�ij��������Ӳ������ʱ,Ͷ��m��,���泯����n�� ,������˵������ȷ����(����)
,������˵������ȷ����(����)
A. Pһ������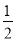
B. Pһ��������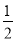
C. ��Ͷһ��,P���ӽ�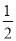
D. ��Ͷ������������,P��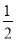 �����ڶ�
�����ڶ�
 D
������������Ƶ�ʹ��Ƹ���ʱ��ֻ�д������飬������Ƶ�ʹ��Ƹ��ʡ���ΪӲ��ֻ���������棬����Ͷ��ʱ���泯�ϵĸ���Ϊ���������Ͷ�����������ӣ��ȶ��ڸ���.
��ѡD.
D
������������Ƶ�ʹ��Ƹ���ʱ��ֻ�д������飬������Ƶ�ʹ��Ƹ��ʡ���ΪӲ��ֻ���������棬����Ͷ��ʱ���泯�ϵĸ���Ϊ���������Ͷ�����������ӣ��ȶ��ڸ���.
��ѡD. ��ͼ,�������Բ�����Ϊ58��,����Ӱ���ֵ����Ϊ(����)
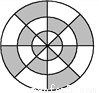
A. 58�� B. 29�� C. 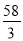 �� D.
�� D. 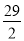 ��
��
 B
������������ͼ�ο��Կ�����Ӱ���ֵ�������������һ�룬
��Ӱ���ֵ����=��58��=29�У�
��ѡB��
B
������������ͼ�ο��Կ�����Ӱ���ֵ�������������һ�룬
��Ӱ���ֵ����=��58��=29�У�
��ѡB�� ��12�֣���a��b��Ϊ�෴����b��c��Ϊ������������m������������������
��1������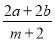 ��acֵ��
��acֵ��
��2����a��1����m=��1��S=|2a��3b|��2|b��m|��|b+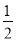 |������4��2a��S��+2��2a��S������2a��S����ֵ��
|������4��2a��S��+2��2a��S������2a��S����ֵ��
��3����m��0����xΪ������ʱ��|x+m|��|x��m|+1�Ƿ�������ֵ�������ڣ����������ֵ�������x��ȡֵ��Χ���������ڣ���˵�����ɣ�
 ��1��-1����2������3����xʱ,ȡ���ֵΪ3
�������������������1���ȸ���a��b��Ϊ�෴����b��c��Ϊ�������ó�a+b=0��bc=1���ٴ����������ʽ���м��㣻
��2������a��1��m������������������S���л����ٴ����������ʽ���м��㣻
��3��������m>0����֪m=1����m=1ʱ������|x+m|-|x-m|+1���ٸ��ݾ���ֵ������ȥ������ֵ���ţ��������ʽ��ֵ��
����...
��1��-1����2������3����xʱ,ȡ���ֵΪ3
�������������������1���ȸ���a��b��Ϊ�෴����b��c��Ϊ�������ó�a+b=0��bc=1���ٴ����������ʽ���м��㣻
��2������a��1��m������������������S���л����ٴ����������ʽ���м��㣻
��3��������m>0����֪m=1����m=1ʱ������|x+m|-|x-m|+1���ٸ��ݾ���ֵ������ȥ������ֵ���ţ��������ʽ��ֵ��
����... ��֪ab��0,|a|=2,|b|=7,��a+b=________��
 9��-9
����������|a|=2,|b|=7,
��a=��2,b=��7,
��ab��0,
��a��bͬ�ţ�
��a=2,b=7�� a=-2,b=-7,
��a=+b=2+7=9�� a+b=-2-7=-9.
9��-9
����������|a|=2,|b|=7,
��a=��2,b=��7,
��ab��0,
��a��bͬ�ţ�
��a=2,b=7�� a=-2,b=-7,
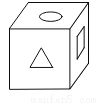
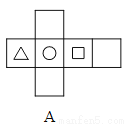
��a=+b=2+7=9�� a+b=-2-7=-9. �����ĸ�ͼ���У������۵���Χ����ͼ1��ֻ����������ӡ��ͼ����������ֽ�е��ǣ� ��
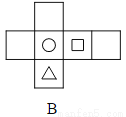
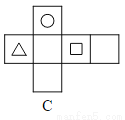
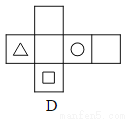
 B
�����������⿼������������չ��ͼ
����ͼ�з���������λ�ù�ϵ����
������ͼ���Ķ���Ӧ��Բ�ε�ͼ����ԣ���ѡ��A��C��˲��������Դ���
������ͼ�����ڵ���Ӧ��Բ�ε�ͼ�����ڵ������ڣ���ѡ��D���Ҳ��������ȷ����B��
��ѡB��
B
�����������⿼������������չ��ͼ
����ͼ�з���������λ�ù�ϵ����
������ͼ���Ķ���Ӧ��Բ�ε�ͼ����ԣ���ѡ��A��C��˲��������Դ���
������ͼ�����ڵ���Ӧ��Բ�ε�ͼ�����ڵ������ڣ���ѡ��D���Ҳ��������ȷ����B��
��ѡB�� ��ͼ����֪�߶�AB�Ĵ�ֱƽ����CP��AB�ڵ�P����AP=2PC���������߶�AB����������D��E��ʹ������AD=DC=CE=EB���������¼ס�������������
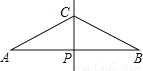
�ף��ֱ�����ACP����BCP��ƽ���ߣ��ֱ�AB��D��E����D��E��Ϊ�����ң��ֱ���AC��BC�Ĵ�ֱƽ���ߣ��ֱ�AB��D��E����D��E���㼴Ϊ��������˵����ȷ���ǣ�������
A. �ס��Ҷ���ȷ B. �ס��Ҷ�����
C. ����ȷ���Ҵ��� D. �״�������ȷ
 D
������������������ף���ȻCP=AP��
����A�١�ACP��
����A�١�ACD���ײ���ȷ��
�ҡ�CP���߶�AB���д��ߣ�
���ABC�ǵ��������Σ���AC=BC����A=��B��
��AC��BC֮�д��߷ֱ�AB��D��E��
���A=��ACD����B=��BCE��
�ߡ�A=��B��
���A=��ACD����B=��BCE��
��AC=BC��
���ACD��...
D
������������������ף���ȻCP=AP��
����A�١�ACP��
����A�١�ACD���ײ���ȷ��
�ҡ�CP���߶�AB���д��ߣ�
���ABC�ǵ��������Σ���AC=BC����A=��B��
��AC��BC֮�д��߷ֱ�AB��D��E��
���A=��ACD����B=��BCE��
�ߡ�A=��B��
���A=��ACD����B=��BCE��
��AC=BC��
���ACD��...